重複組合せの本サイトの解き方を応用して難問を作ってみました。
多分、この問題は絶対に試験には出ないと思いますので、興味のある人だけ読んでください。
【問５】
１，２，３の３つの数字の中から、以下の例外規則以外では同じ数字を複数選べる。例外規則とは、選ぶ数字のうち一番大きい数字は１つしか選ばない。その規則の下で、
数字を３つ選んで作る数字の組合せの数は何個あるか。
この問題の組合せ例をいくつか書くと、
選らんだ数字を左から小さい順に整列して書くと、
（１，１，２）
（１，２，３）
・・・
と順次に書けます。
ただし、問題の条件により、
（２，３，３）はダメです。
（１，２，２）もダメです。
（１，１，１）もダメです。
この整列した組合せの数を求める問題です。
この問題は、その解の組み合せと１対１に対応する別の組み合わせを求める以下の問題を考えます。そして、その組み合わせの数を考えると解けます。
その組合せは、以下の、
数字を直接に指定する３つの指令と、
数字を間接的に指定する１つの指令
とから成る合計４つの指令のうちから３つを選ぶ組合せと１対１対応します。
１選択指令：数字１を選ぶ。
２選択指令：数字２を選ぶ。
３選択指令：数字３を選ぶ。
第２指令：整列表示した、２番目の数字を１番目の数字と同じ数字にする。
上の指令から３つを選ぶ。
（１選択指令、２選択指令、３選択指令）から選ばれた数字選択指令を数字の小さい順に、順番が抜けている第ｎ指令の位置に配置する。
この指令の組合せは、例えば、
（１）１選択指令：数字１を選ぶ。
第２指令：整列表示した、２番目の数字を１番目の数字と同じ数字にする。
（３）３選択指令：数字３を選ぶ。
です。
この指令の組合せの結果、
（１，１，３）の数字の組合せが選ばれます。
また、例えば、
（１）２選択指令：数字２を選ぶ。
第２指令：整列表示した、２番目の数字を１番目の数字と同じ数字にする。
（３）３選択指令：数字３を選ぶ。
この指令の組合せの結果、
（２，２，３）の数字の組合せが選ばれます。
大事なポイントは、この指令の組み合わせが、
「３つの数字の中から以下の例外規則以外では同じ数字を複数選べる。例外規則とは、選ぶ数字のうち一番大きい数字は１つしか選ばない。その規則の下で、数字を３つ選んで作る数字の組合せ」に、
１対１に対応することである。
そのため、
（求める組合せの数）
＝（数字を直接選択する３つの指令と、その他の、数字を間接的に指定する指令１つとから成る合計４つの指令のうちから３つを選ぶ組合せの数）
＝（３＋１）Ｃ３
＝（３＋１）Ｃ１＝４
実際に全部の組合せを書き出してみると、
（１，１，２）
（１，１，３）
（１，２，３）
（２，２，３）
の４つの組合せのみです。
場合の数と確率
リンク：高校数学の目次
佐藤の数学教科書[個数の処理・確率編]の１３６頁に、
以下の例題がありました。
【問４】
１，２，３，４の４つの数字の中から同じ数字を何回も選ぶことを許して、
３つの数字を選ぶ。その数字の組合せの数は何個あるか。
【解答１】
この問題の組合せ例をいくつか書くと、
選んだ数字を左から小さい順に整列して書くと、
（１，１，２）
（２，２，２）
（１，２，４）
（２，３，４）
・・・
と順次に書けます。
この整列した組合せの数を求める問題です。
この問題は、その解の組み合せと１対１に対応する別の組み合わせを求める以下の問題を考えます。そして、その組み合わせの数を考えると解けます。
その組合せは、以下の、
数字を直接に指定する４つの指令と、
数字を間接的に指定する２つの指令
とから成る合計６つの指令のうちから３つを選ぶ組合せと１対１対応します。
１選択指令：数字１を選ぶ。
２選択指令：数字２を選ぶ。
３選択指令：数字３を選ぶ。
４選択指令：数字４を選ぶ。
第２指令：整列表示した、２番目の数字を１番目の数字と同じ数字にする。
第３指令：整列表示した、３番目の数字を２番目の数字と同じ数字にする。
上の指令から３つを選ぶ。
（１選択指令、２選択指令、３選択指令、４選択指令）から選ばれた数字選択指令を数字の小さい順に、順番が抜けている第ｎ指令の位置に配置する。
この指令の組合せは、例えば、
（１）３選択指令：数字３を選ぶ。
第２指令：整列表示した、２番目の数字を１番目の数字と同じ数字にする。
第３指令：整列表示した、３番目の数字を２番目の数字と同じ数字にする。
です。
この指令の組合せの結果、
（３，３，３）の数字の組合せが選ばれます。
また、例えば、
（１）２選択指令：数字２を選ぶ。
第２指令：整列表示した、２番目の数字を１番目の数字と同じ数字にする。
（３）４選択指令：数字４を選ぶ。
この指令の組合せの結果、
（２，２，４）の数字の組合せが選ばれます。
大事なポイントは、この指令の組み合わせが、
４つの数字の中から同じ数字を何回も取ることを許して、１度に３つずつ数字を取って作る組合せに、
１対１に対応することである。
（１）この指令の組み合わせが、１度に３つずつ数字を取って作る組合せを表す。
（２）逆に、１度に３つずつ数字を取って作る組合せは、必ず、これらの指令の３つの組み合わせによって表すことができる。
そのため、
（４つの数字の中から同じ数字を何回も取ることを許して、１度に３つずつ数字を取って作る組合せの数）
＝（数字を直接選択する４つの指令と、その他の、数字を間接的に指定する指令２つとから成る合計６つの指令のうちから３つを選ぶ組合せの数）
＝（４＋２）Ｃ３
（解答おわり）
【解答２】
上図のように数字１の行と２の行と３の行と４の行の４つの行を有し、横の長さが３の格子を考える。格子のＡ点からＢ点まで、数字１の行から４の行まで格子を辿って、右と上に進む最短経路を描く。
上図で、
数字１の数＝（１の行の、Ａ点から昇り階段までの長さ）
数字２の数＝（２の行の、階段と階段の間の長さ）
数字３の数＝（３の行の、階段と階段の間の長さ）
数字４の数＝（４の行の、階段からＢ点までの長さ）
とすると、
Ａ点からＢ点まで、格子をたどって右と上に進む１つの最短経路は、
３個の数字を取る場合の、数字１を取った数と数字２を取った数と数字３を取った数ろ数字４を取った数の１つの組合せに
１対１で対応する。
そのため、Ａ点からＢ点までの全ての経路の数は、
４つの数字の中から同じ数字を何回も取ることを許して、
１度に３つずつ取って作る組合せの数と等しい。
上図の経路は、
→↑→↑→↑
とあらわせる。
図のＡ点からＢ点までの全ての経路の数は、(↑)３つと、(→)３つが作る全ての組み合わせの数と等しい。
その数は、
（３＋３）Ｃ３
＝（３＋３）！／（３！×３！）
＝６×５×４／（３×２）＝２０
になる。
これは、先の解答と同じ答えである。
（解答おわり）
場合の数と確率
リンク：高校数学の目次
答えの正しさを確認しやすいように問題を簡単にしてみました。
【３種の玉から重複を許して２個を選ぶ組み合わせの数】
上図のような３種の玉から、重複を許して２個を選ぶ組み合わせの数を求める。
【解答】
（①の玉の数，②の玉の数，③の玉の数）
の事象の連鎖を考える。
例えば、①の玉を１個、②の玉を１個、③の玉を０個取り出す事象の連鎖は、
（１，１，０）
である。
このようにしてあらわした、３種の玉の数の組み合せを表す事象の連鎖と１対１に対応する以下の経路を考える。
３種の玉から、重複を許して５個を選ぶ組み合わせの数は、その経路の数に等しい。
上図のように①の行と②の行と③の行との３つの行を有し、横の長さが２の格子を考える。格子のＡ点からＢ点まで、①の行から③の行まで格子を辿って、右と上に進む最短経路を描く。
上図で、
玉①の数＝（①行の、Ａ点から昇り階段までの長さ）
玉②の数＝（②行の、階段と階段の間の長さ）
玉③の数＝（③行の、階段からＢ点までの長さ）
とすると、
Ａ点からＢ点まで、格子をたどって右と上に進む１つの最短経路は、
２個の玉を取る場合の、玉①を数と玉②を取った数と玉③を取った１つの組合せに
１対１で対応する。
そのため、Ａ点からＢ点までの全ての経路の数は、３種の玉から、重複を許して２個を選ぶ組み合わせの数と等しい。
上図の経路は、
→↑→↑
とあらわせる。
図のＡ点からＢ点までの全ての経路の数は、(↑)２つと、(→)２つが作る全ての組み合わせの数と等しい。
その数は、
（２＋２）Ｃ２
＝（２＋２）！／（２！×２！）
＝４×３／２＝６
になる。
（解答おわり）
場合の数と確率
リンク：高校数学の目次
【３種の玉から重複を許して５個を選ぶ組み合わせの数】
【問１】
上図のような３種の玉から、重複を許して５個を選ぶ組み合わせの数を求めよ。
【解答】
（①の玉の数，②の玉の数，③の玉の数）
の事象の連鎖を考える。
例えば、①の玉を２個、②の玉を２個、③の玉を１個取り出す事象の連鎖は、
（２，２，１）
である。
このようにしてあらわした、３種の玉の数の組み合せを表す事象の連鎖と１対１に対応する以下の経路を考える。
３種の玉から、重複を許して５個を選ぶ組み合わせの数は、その経路の数に等しい。
上図のように①の行と②の行と③の行との３つの行を有し、横の長さが５の格子を考える。格子のＡ点からＢ点まで、①の行から③の行まで格子を辿って、右と上に進む最短経路を描く。
上図で、
①の数＝（①行の、Ａ点から昇り階段までの長さ）
②の数＝（②行の、階段と階段の間の長さ）
③の数＝（③行の、階段からＢ点までの長さ）
とすると、
Ａ点からＢ点まで、格子をたどって右と上に進む１つの最短経路は、
５個の玉を取り、①を取った数と②を取った数と③を取った数の１つの組合せに
１対１で対応する。
その対応の特殊な例では、
①の数が５、②の数が０、③の数が０の組み合わせは、下の図の経路に対応する。
①の数が０、②の数が０、③の数が５の組み合わせは、下の図の経路に対応する。
そのため、Ａ点からＢ点までの全ての経路の数は、
３種の玉から、重複を許して５個を選ぶ組み合わせの数と等しい。
上図の経路は、
→→↑→→↑→
とあらわせる。
すなわち、経路は、(↑)２つと(→)５つの順列であらわされる。
（Ａ点からＢ点までの経路は、(↑)２つと(→)５つの順列と１対１対応する）
そのため、図のＡ点からＢ点までの全ての経路の数は、(↑)２つと、(→)５つが作る全ての順列の数と等しい。
その数は、
（２＋５）！／（２！×５！）
＝（２＋５）Ｃ２＝（２＋５）Ｃ５
になる。
（解答おわり）
場合の数と確率
リンク：高校数学の目次
リンク：問１０
円順列とじゅず順列の数を求めます。
以下の問題はかなり難しい（特に、じゅず順列の数の計算）ので、無理して読む必要は無いと思います。
この問題より先に、問１０をやってください。
この問９は、どうしても読みたい人だけ読めば良いと考えます。
【問９】
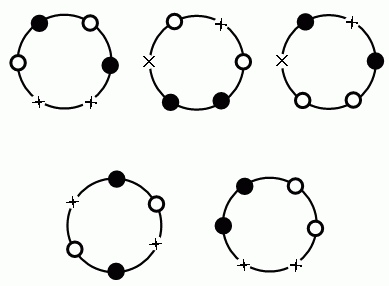
（１）×２個と●２個と○４個を円形に並べる方法（円順列）は何通りあるか。
（２）更に、それらを連結したじゅずを作る方法（じゅず順列）は何通りあるか。
（１）先ず、円順列の数を求めます。
〔解１〕
×と●と○を並べる席が２＋２＋４＝８箇所あります。
８つの席が固定されているならば、×２つと●２つと残り４つを並べる組み合わせの数は、
８！／（４！×２！×２！）＝８Ｐ４／（２！×２！）
＝８×７×６×５／（２×２）＝４２０通り
あります。
×と●と○の１つの円順列の配置を回転させると、固定した席に対しては８倍の異なる配置になる場合があります。
固定した席への配置する場合の数の４２０通りの配置のうち、１つの円順列の配置を回転させて８倍の配置ができる場合については、その場合の数を８で割り算して円順列の数を数えます。
（第１のタイプの配置）
下の３つの円順列の配置では、１／２回転で元の形と同じ形になります。
このタイプの配置では、１つの円順列の配置を回転させて４倍の配置ができます。
この３つの円順列の配置以外では、１回転の数分の１の回転で元の形と同じ形になるものはありません。
第１のタイプ以外の配置では、１回転で元の形に戻る配置であって、円順列で１つと数えられる配置を回転して（固定した席では）８倍の配置ができます。
第１のタイプ以外の円順列の数は、
第１のタイプ以外の円順列の数
＝（固定席での全部の配置の数－（第１のタイプの円順列の数×４））／８
＝（４２０－（３×４））／８＝４０８／８＝５１
一方、第１のタイプの円順列の数は３組でした。
よって、全部の円順列の数は、
５１＋３＝５４
組みです。
（解１おわり）
〔解２〕
以下のように考えて解くことができます。
（第１のタイプの配置：(1/2)回転で元の形と同じ形になる配置）
(1/2)回転すると元の形に戻る第１のタイプの配置パターンの場合は、上図のように、黒玉●については、黒玉●が、元の位置から(1/2)回転した位置にもあるように繰り返して存在し、結局、黒玉●が中心対称な位置に２個ある配置パターンになる。第１のタイプの配置パターンは、そのように、各色の玉が中心対称な位置にある配置パターンである。
第１のタイプの配置パターンは、配置パターンの円の１／２の部分の、４個の玉の部分が１周期になって、それが２回繰り替えされて全ての玉の配置が決まる配置パターンである。
そのため、第１のタイプの玉の配置は、席が固定された場合の配置の数は、１周期である、円順列の円の１／２の部分の４個の玉の並べ方の数で計算する。その数は、上図のように１個の×の位置を固定して考え、その配置の数は１個の●の位置のバラエティの数である。その数は上図のように３組ある。
第１のタイプの配置パターンは、１／８回転する毎に、固定した席に対しては、異なる配置になり、１周期である１／２回転するまでに、0回転、(1/8)回転、(2/8)回転、(3/8)回転、した場合の４つの異なる配置が作られる。
席を固定した場合の、第１のタイプの配置のパターンの数は、席を固定しない場合の配置パターンの数３の４倍になる。その数は：
３×４＝１２
個である。
（１回転すると元の形に戻る（全部の）配置）
１回転して元の形になる全ての配置パターンには、第１のタイプの配置が含まれる。 全配置パターンの、席が固定された場合の配置の数は、以下のように計算する。
×と●と○を並べる席が２＋２＋４＝８箇所ある。
８つの席が固定されているならば、×２つと●２つと残り４つを並べる組み合わせの数は、
８！／（４！×２！×２！）＝８Ｐ４／（２！×２！）
＝８×７×６×５／（２×２）＝４２０個
ある。
（第１のタイプ以外の配置：１回転して初めて元の形に戻る配置）
全部の組合せの数から、第１のタイプの配置パターンの数を引き算することで、１回転して初めて元の形に戻る、（席を固定した場合の）配置の数を求める。その数は：
４２０－（３×４）＝４０８
個ある。
この、第１のタイプ以外の配置パターンは、１／８回転する毎に、固定した席に対しては、異なる配置になる。すなわち、１周期である１回転するまでに、0回転、(1/8)回転、(2/8)回転、(3/8)回転、(4/8)回転、(5/8)回転、(6/8)回転、(7/8)回転した８つの場合で８つの異なる配置が作られる。
席を固定しない場合の、この第１のタイプ以外の配置の数は、席を固定した場合の配置の数４０８の８分の１になる。その数は：
４０８／８＝５１
組ある。
（全部の円順列の数）
以上の合計の、席を固定しない場合の、全部の円順列の配置パターンの数は：
３＋５１＝５４
組ある。
（解２おわり）
（２）次に、じゅず順列の数を求めます。
じゅず順列の場合の数を計算するには、円順列の配置毎に、
円の中心を通る裏返し線でその円順列の配置を対称に裏返して、
それが、裏返す前と同じ円順列の配置になる配置があるかどうかを調べます。
（第２のタイプ：線対称な配置）
下の１２の配置は、円の中心と×の配置の中間を通る裏返し線に関して対称な形であって、
裏返し線で裏返した配置の形が元の配置と同じ形になるタイプの配置です。
この第２のタイプの円順列は１２個のみです。
第２のタイプ以外の配置では、線対称な形では無いので、裏返した形は、元の形を回転することでは作れません。
第２のタイプ以外の円順列の配置は、元の配置と、裏返した後の配置とは異なる２個の配置と数えられています。
このように、第２のタイプ以外の配置は、円順列では２倍に数えられているので、
第２のタイプ以外の配置の、じゅず順列の数は、倍率である２で割り算して求められ、その数は、
（５４－１２）／２＝２１
あります。
一方、第２のタイプのじゅず順列の数は１２個でした。
そのため、全部のじゅず順列の数は、
じゅず順列の数＝２１＋１２＝３３
場合の数と確率
リンク：高校数学の目次
円順列とじゅず順列の数を求めます。
【問８】
（１）×２個と●２個と○３個を円形に並べる方法（円順列）は何通りあるか。
（２）更に、それらを連結したじゅずを作る方法（じゅず順列）は何通りあるか。
（１）先ず、円順列の数を求めます。
×と●と○を並べる席が２＋２＋３＝７箇所あります。
７つの席が固定されているならば、×２つと●２つと残り３つを並べる組み合わせの数は、
７！／（３！×２！×２！）＝７Ｐ４／（２！×２！）
＝７×６×５×４／（２×２）＝２１０通り
あります。
--------補足------------
この計算は、以下のように計算することもできます。
７！／（３！×２！×２！）＝７！／（２！×２！×３！）
＝（７Ｃ２）（５Ｃ２）
＝（７×６）（５×４）／（２×２）＝２１０通り
-------補足おわり-------
玉×と●と○の１つの円順列の配置を回転させると、固定した席に対しては７倍の異なる配置になります。
もし１回転の数分の１の回転で元の形と同じ形になる配置があれば、それは７倍とは異なる倍数の配置ができますが、
この問題の場合では、１回転の数分の１の回転で元の形と同じ形になるものはありません。
そのため、固定した席への配置する場合の数の２１０通りの配置の数は、１つの円順列の配置を回転してできる７倍の配置の数であるので、その配置の数２１０を７で割り算して円順列の数を数えます。
よって、全部の円順列の数は、
円順列の数＝２１０／７＝３０
です。
（２）次に、じゅず順列の数を求めます。
じゅず順列の場合の数を計算するには、円順列の配置毎に、
円の中心を通る裏返し線でその円順列の配置を対称に裏返して、
それが、裏返す前と同じ円順列の配置になる配置があるかどうかを調べます。
（第１のタイプ：線対称な配置）
下の６つの形の配置は、円の中心と×の配置の中間点を通る裏返し線を配置の中心軸にすれば、
裏返し線で裏返した配置の形を、元の配置と同じ形にできる線対称な形の配置です。
この第１のタイプの配置は６個のみです。
第１のタイプ以外の配置では、線対称では無いので、それを裏返した形は、元の形を回転することでは作れません。
円順列では、第１のタイプ以外の配置では、元の配置と、裏返した後の配置とは異なる２個の配置と数えられています。
このように、第１のタイプ以外の配置は、円順列では２倍に数えられているので、
第１のタイプ以外の配置の、じゅず順列の数は、倍率である２で割り算して求められ、その数は、
第１のタイプ以外のじゅず順列の数
＝（全部の円順列の数－第１のタイプの円順列の数）／２
＝（３０－６）／２＝１２
あります。
一方、第１のタイプのじゅず順列の数（＝円順列の数）は６個でした。
そのため、全部のじゅず順列の数は、
じゅず順列の数＝１２＋６＝１８
場合の数と確率
リンク：高校数学の目次
円順列とじゅず順列の数を求めます。
【問７】
（１）●３個と○４個を円形に並べる方法（円順列）は何通りあるか。
（２）更に、それらを連結したじゅずを作る方法（じゅず順列）は何通りあるか。
（１）先ず、円順列の数を求めます。
玉●と○を並べる席が３＋４＝７箇所あります。
７つの席が固定されているならば、玉●３つを並べる組み合わせの数は、
７Ｃ３＝７×６×５／（３×２）＝３５通り
あります。
席への●と○の１つの円順列の配置は、１回転して元の形に戻り、その間の１／７ずつの回転では、固定した席に対しては異なる７つの配置になります。
そのため、席を固定して配置した場合の数は、１つの配置が回転した数がだぶって数えられています。
この問題の場合に、回転することによってできる配置の数は７倍あります。
１つの回転から７倍の配置ができる組み合わせの数は、固定した席の組み合わせの数を７で割り算して数えます。
それは下の図のような●の配置の場合です。
もし、１回転の数分の１の回転で元の形と同じ形になる配置があれば、それは７倍とは異なる倍数の配置ができますが、
この問題の場合では、１回転の数分の１の回転で元の形と同じ形になるものはありません。
つまり、この問題の場合では、席を固定した場合のどの配置も、円順列で１つと数えられる配置を回転して７倍になった配置であって、全て同じタイプの配置です。
よって、全部の円順列の数は、
円順列の数＝３５／７＝５
（２）次に、じゅず順列の数を求めます。
じゅず順列の場合の数を計算するには、円順列の配置毎に、
円の中心を通る裏返し線でその円順列の配置を対称に裏返して、
それが、異なる円順列の配置になるかどうかを調べます。
（第１のタイプ：線対称な配置）
下の形の配置は、円の中心を通る裏返し線を配置の中心軸にすれば、
裏返し線で裏返した配置の形を、元の配置と同じ形にできるタイプの配置です。
この第１のタイプの配置は３個あります。
第１のタイプ以外の配置（線対称では無い配置）では、その配置を裏返し線で裏返した形は、元の形を回転することでは作れません。
円順列では、第１のタイプ以外の配置では、元の配置と、裏返した後の配置とは異なる２個の配置と数えられています。
このように、第１のタイプ以外の配置は、円順列では２倍に数えられているので、
第１のタイプ以外の配置の、じゅず順列の数は、倍率である２で割り算して求められ、その数は、
（５－３）／２＝１
あります。
一方、第１のタイプのじゅず順列の数は３個でした。
そのため、全部のじゅず順列の数は、
じゅず順列の数＝１＋３＝４
場合の数と確率
リンク：高校数学の目次
円順列とじゅず順列の数を求めます。
【問６】
（１）×１個と●２個と○４個を円形に並べる方法（円順列）は何通りあるか。
（２）更に、それらを連結したじゅずを作る方法（じゅず順列）は何通りあるか。
（１）先ず、円順列の数を求めます。
この問題では、×が１個のみです。
このように、ある形の玉が１個のみの問題の考えかたは、以下のようにします。
つまり、その１個のみの玉×を円の最上部に固定して考えます。
円順列の数は、残りの●２個と○４個を並べる組み合わせの数になります。
●の位置を定めると残りの○の位置が自動的に決まりますので、●の配置の数だけを求めれば、
円順列の数が求められます。
その配置の数は、
６Ｃ２＝６×５／２＝１５通り
あります。
そのため、全部の円順列の数は、
円順列の数＝１５
（２）次に、じゅず順列の数を求めます。
じゅず順列の場合の数を計算するには、円順列の配置毎に、
円の中心と玉×を通る裏返し線でその円順列の配置を対称に裏返して、
それが、異なる円順列の配置になるかどうかを調べます。
（第１のタイプ：線対称な配置）
下の３つの形の場合は、×と円の中心を通る線で円順列の配置を裏返してできる配置の形が、元の配置と同じ形になります。
この（第１のタイプの配置の）円順列は３つしかありません。
（第２のタイプ：線対称で無い配置）
第２のタイプの円順列の配置は、裏返してできる配置の形が、元の配置と同じ形にならない。
その配置は、元の形と、それを裏返した形が別の配置として２個と数えられています。
そのため、第２のタイプの円順列に対応する、第２のタイプのじゅず順列の数は、
｛（全ての円順列の数）－（第１のタイプ以外のじゅず順列の数）｝＝（第２のタイプの円順列の数）
を２個で割り算した数であり、以下の式で計算できる。
第２のタイプのじゅず順列の数＝
＝（６Ｃ２－３）／２
＝（１５－３）／２
＝６
である。
一方、第１のタイプのじゅず順列の数＝３
です。
そのため、全部のじゅず順列の数は、
全部のじゅず順列の数＝
＝６＋３
＝９
場合の数と確率
リンク：高校数学の目次
円順列とじゅず順列の数を求めます。
【問５】
（１）玉×１個と●２個と○３個を円形に並べる方法（円順列）は何通りあるか。
（２）更に、それらを連結したじゅずを作る方法（じゅず順列）は何通りあるか。
（１）先ず、円順列の数を求めます。
この問題では、玉×が１個のみです。
このように、ある形の玉が１個のみの問題の考えかたは、以下のようにします。
つまり、その１個のみの玉×を円の最上部に固定して考えます。
円順列の数は、残りの●２個と○３個を並べる組み合わせの数になります。
●の位置を定めると残りの○の位置が自動的に決まりますので、●の配置の数だけを求めれば、
円順列の数が求められます。
その配置の数は、
５Ｃ２＝５×４／２＝１０通り
あります。
そのため、全部の円順列の数は、
円順列の数＝１０
（２）次に、じゅず順列の数を求めます。
じゅず順列の場合の数を計算するには、円順列の配置毎に、
円の中心と×を通る線でその円順列の配置を対称に裏返して、
それが、異なる円順列の配置になるか（配置が線対称では無いか）どうかを調べます。
（第１のタイプ：線対称な配置）
下の２つの形の場合は、×と円の中心を通る線で円順列の配置を裏返してできる配置の形が、元の配置と同じ形になる、線対称な形の配置です。この配置では、じゅず順列の配置の数が円順列の配置の数と同じです。
この（第１のタイプの配置の）円順列の配置の数は２つしかありません。
（第２のタイプ：線対称では無い配置）
第２のタイプの配置は、線対称では無く、裏返してできる配置の形が、元の配置と同じ形にならない。
その配置は、元の形と、それを裏返した形が別の配置として２個に数えられています。
そのため、第２のタイプの配置の、じゅず順列の数は、
第２のタイプのじゅず順列の配置の数＝
＝第２のタイプの円順列の配置の数／２
＝（全ての円順列の配置の数－第１のタイプの配置の数）／２
＝（５Ｃ２－２）／２＝（１０－２）／２＝４
一方、第１のタイプのじゅず順列の配置の数＝２
です。
そのため、全部のじゅず順列の数は、
じゅず順列の数＝４＋２＝６
場合の数と確率
リンク：高校数学の目次
円順列とじゅず順列の数を求めます。
【問４】
（１）×１個と●１個と○４個を円形に並べる方法（円順列）は何通りあるか。
（２）更に、それらを連結したじゅずを作る方法（じゅず順列）は何通りあるか。
（１）先ず、円順列の数を求めます。
この問題では、玉×が１個のみです。
このように、ある形の玉が１個のみの問題の考えかたは、以下のようにします。
つまり、その１個のみの玉×を円の最上部に固定して考えます。
円順列の数は、残りの●１個と○４個を並べる組み合わせの数になります。
●の位置を定めると残りの○の位置が自動的に決まりますので、●の配置の数だけを求めれば、
円順列の数が求められます。
その配置の数は、
５Ｃ１＝５通り
あります。
そのため、全部の円順列の数は、
円順列の数＝５
（２）次に、じゅず順列の数を求めます。
じゅず順列の場合の数を計算するには、円順列の配置毎に、
円の中心と玉×とを通る裏返し線でその円順列の配置を対称に裏返して、
それが、異なる円順列の配置になるか（配置が線対称では無いか）どうかを調べます。
（第１のタイプ：線対称な配置）
下の形の場合は、×と円の中心を通る線で円順列の配置を裏返してできる配置の形が、元の配置と同じ形になります。
この（第１のタイプの）円順列の数は、じゅず順列の数と同じです。
この第１のタイプのじゅず順列の数は１つしかありません。
（第２のタイプ：線対称では無い配置）
第２のタイプ（線対称な配置）を裏返し線で裏返してできる（円順列の）配置の形は、元の配置を回転して作る全ての配置と異なる形の配置になります。
つまり、第２のタイプの配置では、円順列の配置の数がじゅず順列の配置の数の２倍あります。
そのため、第２のタイプのじゅず順列の配置の数は、そのタイプの円順列の配置の数を２で割り算することで計算でき、
第１のタイプ以外のじゅず順列の数
＝（全部の円順列の数－第１のタイプの円順列の数）／２
＝（５Ｃ１－１）／２＝（５－１）／２＝２
一方、第１のタイプのじゅず順列の数＝１
であるため、全部のじゅず順列の数は、
じゅず順列の数＝２＋１＝３
場合の数と確率
リンク：高校数学の目次
円順列とじゅず順列の数を求めます。
【問３】
（１）●３個と〇３個を円形に並べる方法（円順列）は何通りあるか。ただし、円順列において、●同士を区別せず、〇同士を区別しないものとする。
（２）更に、それらを連結したじゅずを作る方法（じゅず順列）は何通りあるか。
【問３】（１）の解答
先ず、円順列の数を求めます。
〔解１〕
玉●と○を並べる席が３＋３＝６箇所あります。
６つの席を固定した場合の、玉●３つを並べる組み合わせの数は、
６Ｃ３＝６×５×４／（３×２）＝２０通り
あります。
席への玉●と○の１つの配置を回転させると、席を固定した場合は異なる配置になります。
そのため、席を固定した場合の配置の数は、元の配置が回転した数がだぶって数えられています。
（第１のタイプ：１回転すると元の形に戻る配置）
上図の形の配置の場合に、１回転すると元の形に戻る。これが第１のタイプの配置です。
この配置（元の配置）を１／６回転する毎に（席を固定した配置では）異なる配置になり、６つの配置ができる。
第１のタイプの配置において、固定した席での配置の数を６で割り算した数が、回転しても重ならない元の配置の数になる。
（第２のタイプ：１／３回転すると元の形に戻る配置）
上図の形の配置の場合、１／３回転すると元の形に戻る。これが第１のタイプの配置です。この配置を１／６回転すると、２つの配置ができる。第２のタイプの配置において、固定した席での配置の数を２で割り算した数が、回転しても重ならない元の配置の数になる。この第２のタイプの配置の円順列の数は上図に示した１つのみです。
一方、玉●と玉○が３つずつの円順列の配置では、
２分の１回転で元の形と同じ形になるものは無い。
（第１のタイプの配置の数）
第２のタイプの配置以外が第１のタイプの配置なので、（席を固定した場合の）第１のタイプの配置の数は、
（席を固定した場合の）第１のタイプの配置の数
＝（全部の配置の数）－（第２のタイプの配置の数）
＝６Ｃ３－（１×２）＝２０－２＝１８
です。
（第１のタイプの配置の円順列の数）
（席を固定した場合の）第１のタイプの配置の数を６で割り算することで、第１のタイプの配置の円順列の数が得られます。
第１のタイプの配置の円順列の数＝１８／６＝３
（全部の円順列の数）
一方、第２のタイプの配置の円順列の数は１個でした。
そのため、全部の円順列の数は、
円順列の数＝３＋１＝４
個ある。
（解１おわり）
〔解２〕
以下のように考えて解くことができます。
第２のタイプの配置の数から先に求めます。
（第２のタイプ：(1/3)回転すると元の形に戻る配置）
１／３回転すると元の形に戻る第２のタイプの配置パターンの場合は、上図のように、黒玉●については、黒玉●が、元の位置から(1/3)回転した位置にもあり、(2/3)回転した位置にもあるように繰り返して存在し、結局、黒玉●が三角形状に３個ある配置パターンになる。第２のタイプの配置パターンは、そのように、各色の玉が三角形状の形にある配置パターンである。
第２のタイプの配置パターンは、配置パターンの円の１／３の、２個の玉で構成される部分が１周期になって、それが繰り替えされて全ての玉の配置が決まる配置パターンである。
そのため、第２のタイプの玉の配置は、席が固定された場合の配置の数は、１周期である、円順列の円の１／３の部分の２個の玉の並べ方の数で計算する。その数は、２Ｃ１個＝２個ある。
第２のタイプの配置パターンは、１／６回転する毎に、固定した席に対しては、異なる配置になり、１周期である１／３回転するまでに、0回転、(1/6)回転した場合の２つの異なる配置が作られる。
席を固定しない場合の、第２のタイプの配置のパターンの数は、席を固定した場合の配置パターンの数（２Ｃ１）の２分の１になる。その数は：
（２Ｃ１）／２＝１
個ある。
（１回転すると元の形に戻る（全部の）配置）
１回転して元の形になる全ての配置パターンには、第２のタイプの配置が含まれる。 全配置パターンの、席が固定された場合の配置の数は、６Ｃ３＝２０個ある。
この数から、第２のタイプの配置パターンの数を引き算することで、１回転して初めて元の形に戻る第１のタイプの、（席を固定した場合の）配置の数を求める。その数は：
６Ｃ３－２Ｃ１＝１８
個ある。
この、引き算した結果である、第１のタイプの配置パターンは、１／６回転する毎に、固定した席に対しては、異なる配置になり、１周期である１回転するまでに、0回転、(1/6)回転、(2/6)回転、(3/6)回転、(4/6)回転、(5/6)回転した場合の６つの異なる配置が作られる。
席を固定しない場合の、この第１の配置のパターンの数は、席を固定した場合の配置パターンの数（６Ｃ３－２Ｃ１）の６分の１になる。その数は：
（６Ｃ３－２Ｃ１）／６＝３
個ある。
（全部の円順列の数）
以上の合計の、席を固定しない場合の、全部の円順列の配置パターンの数は：
１＋３＝４
個ある。
（解２おわり）
【問３】（２）の解答
次に、じゅず順列の数を求めます。
じゅず順列の場合の数を計算するには、円順列の配置毎に、
円の中心を通る裏返し線に関してその円順列の配置を対称な形に裏返して、
それが、異なる円順列の配置になるかどうかを調べます。すなわち、その配置が線対称では無いか、線対称であるかを調べます。
（第３のタイプ：線対称で無い配置）
下の形の配置の場合は、配置を裏返してできる形が、元の配置を回転することではできない形になります。
円配列では、この形と、これを裏返した形が別の配置として２個と数えられています。
（第４のタイプ：線対称な配置）
それ以外の形の配置は、裏返した形が、元の配置を回転しても作れます。
すなわち、３つの●の配置の中点と円の中心を通る裏返し線で裏返した形は、裏返す前の配置と重なる同じ形になります。
これを第４のタイプの配置と呼びます。
このような対称な形の配置は以下の２つのみです。
第４のタイプの配置（線対称な配置）はじゅず順列でも円順列でも同じ２個の数と数えられています。
第３のタイプのじゅず順列の配置は円順列では２倍に数えられています。
そのため、第３のタイプのじゅず順列の数は、
第３のタイプのじゅず順列の数＝
｛円順列の総数－（第４のタイプのじゅず順列の数）｝／２
＝（４－２）／２＝１
一方、第４のタイプのじゅず順列の数は２個です。
そのため、じゅず順列の数は、
じゅず順列の数＝１＋２＝３
場合の数と確率
リンク：高校数学の目次
