円順列とじゅず順列の数を求めます。
【問３】
（１）●３個と〇３個を円形に並べる方法（円順列）は何通りあるか。ただし、円順列において、●同士を区別せず、〇同士を区別しないものとする。
（２）更に、それらを連結したじゅずを作る方法（じゅず順列）は何通りあるか。
【問３】（１）の解答
先ず、円順列の数を求めます。
〔解１〕
玉●と○を並べる席が３＋３＝６箇所あります。
６つの席を固定した場合の、玉●３つを並べる組み合わせの数は、
６Ｃ３＝６×５×４／（３×２）＝２０通り
あります。
席への玉●と○の１つの配置を回転させると、席を固定した場合は異なる配置になります。
そのため、席を固定した場合の配置の数は、元の配置が回転した数がだぶって数えられています。
（第１のタイプ：１回転すると元の形に戻る配置）
上図の形の配置の場合に、１回転すると元の形に戻る。これが第１のタイプの配置です。
この配置（元の配置）を１／６回転する毎に（席を固定した配置では）異なる配置になり、６つの配置ができる。
第１のタイプの配置において、固定した席での配置の数を６で割り算した数が、回転しても重ならない元の配置の数になる。
（第２のタイプ：１／３回転すると元の形に戻る配置）
上図の形の配置の場合、１／３回転すると元の形に戻る。これが第１のタイプの配置です。この配置を１／６回転すると、２つの配置ができる。第２のタイプの配置において、固定した席での配置の数を２で割り算した数が、回転しても重ならない元の配置の数になる。この第２のタイプの配置の円順列の数は上図に示した１つのみです。
一方、玉●と玉○が３つずつの円順列の配置では、 ２分の１回転で元の形と同じ形になるものは無い。
（第１のタイプの配置の数）
第２のタイプの配置以外が第１のタイプの配置なので、（席を固定した場合の）第１のタイプの配置の数は、
（席を固定した場合の）第１のタイプの配置の数
＝（全部の配置の数）－（第２のタイプの配置の数）
＝６Ｃ３－（１×２）＝２０－２＝１８
です。
（第１のタイプの配置の円順列の数）
（席を固定した場合の）第１のタイプの配置の数を６で割り算することで、第１のタイプの配置の円順列の数が得られます。
第１のタイプの配置の円順列の数＝１８／６＝３
（全部の円順列の数）
一方、第２のタイプの配置の円順列の数は１個でした。
そのため、全部の円順列の数は、
円順列の数＝３＋１＝４
個ある。
（解１おわり）
〔解２〕
以下のように考えて解くことができます。
第２のタイプの配置の数から先に求めます。
（第２のタイプ：(1/3)回転すると元の形に戻る配置）
１／３回転すると元の形に戻る第２のタイプの配置パターンの場合は、上図のように、黒玉●については、黒玉●が、元の位置から(1/3)回転した位置にもあり、(2/3)回転した位置にもあるように繰り返して存在し、結局、黒玉●が三角形状に３個ある配置パターンになる。第２のタイプの配置パターンは、そのように、各色の玉が三角形状の形にある配置パターンである。
第２のタイプの配置パターンは、配置パターンの円の１／３の、２個の玉で構成される部分が１周期になって、それが繰り替えされて全ての玉の配置が決まる配置パターンである。
そのため、第２のタイプの玉の配置は、席が固定された場合の配置の数は、１周期である、円順列の円の１／３の部分の２個の玉の並べ方の数で計算する。その数は、２Ｃ１個＝２個ある。
第２のタイプの配置パターンは、１／６回転する毎に、固定した席に対しては、異なる配置になり、１周期である１／３回転するまでに、0回転、(1/6)回転した場合の２つの異なる配置が作られる。
席を固定しない場合の、第２のタイプの配置のパターンの数は、席を固定した場合の配置パターンの数（２Ｃ１）の２分の１になる。その数は：
（２Ｃ１）／２＝１
個ある。
（１回転すると元の形に戻る（全部の）配置）
１回転して元の形になる全ての配置パターンには、第２のタイプの配置が含まれる。 全配置パターンの、席が固定された場合の配置の数は、６Ｃ３＝２０個ある。
この数から、第２のタイプの配置パターンの数を引き算することで、１回転して初めて元の形に戻る第１のタイプの、（席を固定した場合の）配置の数を求める。その数は：
６Ｃ３－２Ｃ１＝１８
個ある。
この、引き算した結果である、第１のタイプの配置パターンは、１／６回転する毎に、固定した席に対しては、異なる配置になり、１周期である１回転するまでに、0回転、(1/6)回転、(2/6)回転、(3/6)回転、(4/6)回転、(5/6)回転した場合の６つの異なる配置が作られる。
席を固定しない場合の、この第１の配置のパターンの数は、席を固定した場合の配置パターンの数（６Ｃ３－２Ｃ１）の６分の１になる。その数は：
（６Ｃ３－２Ｃ１）／６＝３
個ある。
（全部の円順列の数）
以上の合計の、席を固定しない場合の、全部の円順列の配置パターンの数は：
１＋３＝４
個ある。
（解２おわり）
【問３】（２）の解答
次に、じゅず順列の数を求めます。
じゅず順列の場合の数を計算するには、円順列の配置毎に、
円の中心を通る裏返し線に関してその円順列の配置を対称な形に裏返して、
それが、異なる円順列の配置になるかどうかを調べます。すなわち、その配置が線対称では無いか、線対称であるかを調べます。
（第３のタイプ：線対称で無い配置）
下の形の配置の場合は、配置を裏返してできる形が、元の配置を回転することではできない形になります。
円配列では、この形と、これを裏返した形が別の配置として２個と数えられています。
（第４のタイプ：線対称な配置）
それ以外の形の配置は、裏返した形が、元の配置を回転しても作れます。
すなわち、３つの●の配置の中点と円の中心を通る裏返し線で裏返した形は、裏返す前の配置と重なる同じ形になります。
これを第４のタイプの配置と呼びます。
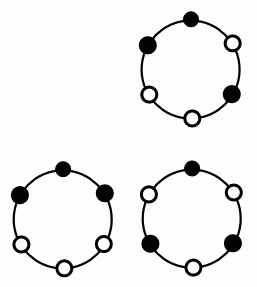
このような対称な形の配置は以下の２つのみです。
第４のタイプの配置（線対称な配置）はじゅず順列でも円順列でも同じ２個の数と数えられています。
第３のタイプのじゅず順列の配置は円順列では２倍に数えられています。
そのため、第３のタイプのじゅず順列の数は、
第３のタイプのじゅず順列の数＝
｛円順列の総数－（第４のタイプのじゅず順列の数）｝／２
＝（４－２）／２＝１
一方、第４のタイプのじゅず順列の数は２個です。
そのため、じゅず順列の数は、
じゅず順列の数＝１＋２＝３
場合の数と確率
リンク：高校数学の目次
【問３】
（１）●３個と〇３個を円形に並べる方法（円順列）は何通りあるか。ただし、円順列において、●同士を区別せず、〇同士を区別しないものとする。
（２）更に、それらを連結したじゅずを作る方法（じゅず順列）は何通りあるか。
【問３】（１）の解答
先ず、円順列の数を求めます。
〔解１〕
玉●と○を並べる席が３＋３＝６箇所あります。
６つの席を固定した場合の、玉●３つを並べる組み合わせの数は、
６Ｃ３＝６×５×４／（３×２）＝２０通り
あります。
席への玉●と○の１つの配置を回転させると、席を固定した場合は異なる配置になります。
そのため、席を固定した場合の配置の数は、元の配置が回転した数がだぶって数えられています。
（第１のタイプ：１回転すると元の形に戻る配置）
第１のタイプの配置において、固定した席での配置の数を６で割り算した数が、回転しても重ならない元の配置の数になる。
（第２のタイプ：１／３回転すると元の形に戻る配置）
一方、玉●と玉○が３つずつの円順列の配置では、 ２分の１回転で元の形と同じ形になるものは無い。
（第１のタイプの配置の数）
第２のタイプの配置以外が第１のタイプの配置なので、（席を固定した場合の）第１のタイプの配置の数は、
（席を固定した場合の）第１のタイプの配置の数
＝（全部の配置の数）－（第２のタイプの配置の数）
＝６Ｃ３－（１×２）＝２０－２＝１８
です。
（第１のタイプの配置の円順列の数）
（席を固定した場合の）第１のタイプの配置の数を６で割り算することで、第１のタイプの配置の円順列の数が得られます。
第１のタイプの配置の円順列の数＝１８／６＝３
（全部の円順列の数）
一方、第２のタイプの配置の円順列の数は１個でした。
そのため、全部の円順列の数は、
円順列の数＝３＋１＝４
個ある。
〔解２〕
以下のように考えて解くことができます。
第２のタイプの配置の数から先に求めます。
（第２のタイプ：(1/3)回転すると元の形に戻る配置）
１／３回転すると元の形に戻る第２のタイプの配置パターンの場合は、上図のように、黒玉●については、黒玉●が、元の位置から(1/3)回転した位置にもあり、(2/3)回転した位置にもあるように繰り返して存在し、結局、黒玉●が三角形状に３個ある配置パターンになる。第２のタイプの配置パターンは、そのように、各色の玉が三角形状の形にある配置パターンである。
第２のタイプの配置パターンは、配置パターンの円の１／３の、２個の玉で構成される部分が１周期になって、それが繰り替えされて全ての玉の配置が決まる配置パターンである。
そのため、第２のタイプの玉の配置は、席が固定された場合の配置の数は、１周期である、円順列の円の１／３の部分の２個の玉の並べ方の数で計算する。その数は、２Ｃ１個＝２個ある。
第２のタイプの配置パターンは、１／６回転する毎に、固定した席に対しては、異なる配置になり、１周期である１／３回転するまでに、0回転、(1/6)回転した場合の２つの異なる配置が作られる。
席を固定しない場合の、第２のタイプの配置のパターンの数は、席を固定した場合の配置パターンの数（２Ｃ１）の２分の１になる。その数は：
（２Ｃ１）／２＝１
個ある。
（１回転すると元の形に戻る（全部の）配置）
１回転して元の形になる全ての配置パターンには、第２のタイプの配置が含まれる。 全配置パターンの、席が固定された場合の配置の数は、６Ｃ３＝２０個ある。
この数から、第２のタイプの配置パターンの数を引き算することで、１回転して初めて元の形に戻る第１のタイプの、（席を固定した場合の）配置の数を求める。その数は：
６Ｃ３－２Ｃ１＝１８
個ある。
この、引き算した結果である、第１のタイプの配置パターンは、１／６回転する毎に、固定した席に対しては、異なる配置になり、１周期である１回転するまでに、0回転、(1/6)回転、(2/6)回転、(3/6)回転、(4/6)回転、(5/6)回転した場合の６つの異なる配置が作られる。
席を固定しない場合の、この第１の配置のパターンの数は、席を固定した場合の配置パターンの数（６Ｃ３－２Ｃ１）の６分の１になる。その数は：
（６Ｃ３－２Ｃ１）／６＝３
個ある。
（全部の円順列の数）
以上の合計の、席を固定しない場合の、全部の円順列の配置パターンの数は：
１＋３＝４
個ある。
（解２おわり）
【問３】（２）の解答
次に、じゅず順列の数を求めます。
じゅず順列の場合の数を計算するには、円順列の配置毎に、
円の中心を通る裏返し線に関してその円順列の配置を対称な形に裏返して、
それが、異なる円順列の配置になるかどうかを調べます。すなわち、その配置が線対称では無いか、線対称であるかを調べます。
（第３のタイプ：線対称で無い配置）
下の形の配置の場合は、配置を裏返してできる形が、元の配置を回転することではできない形になります。
円配列では、この形と、これを裏返した形が別の配置として２個と数えられています。
（第４のタイプ：線対称な配置）
それ以外の形の配置は、裏返した形が、元の配置を回転しても作れます。
すなわち、３つの●の配置の中点と円の中心を通る裏返し線で裏返した形は、裏返す前の配置と重なる同じ形になります。
これを第４のタイプの配置と呼びます。
このような対称な形の配置は以下の２つのみです。
第４のタイプの配置（線対称な配置）はじゅず順列でも円順列でも同じ２個の数と数えられています。
第３のタイプのじゅず順列の配置は円順列では２倍に数えられています。
そのため、第３のタイプのじゅず順列の数は、
第３のタイプのじゅず順列の数＝
｛円順列の総数－（第４のタイプのじゅず順列の数）｝／２
＝（４－２）／２＝１
一方、第４のタイプのじゅず順列の数は２個です。
そのため、じゅず順列の数は、
じゅず順列の数＝１＋２＝３
場合の数と確率
リンク：高校数学の目次
0 件のコメント:
コメントを投稿