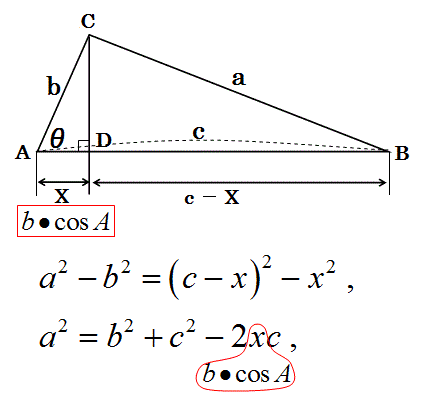佐藤の数学教科書「図形と方程式」編の勉強
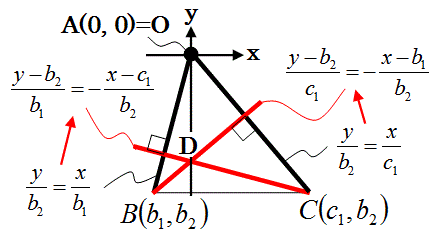
【問】下図のようにA点が原点Oにあり、BCがX座標軸に平行な三角形ABCの座標を図のように定義した上で、その三角形の垂心Dの座標を求めよ。
(1)点あるいはベクトルの座標値を記号であらわすときは、上図の様に添え字を付けて座標記号をあらわし、点の名前BとCを引き継いだ記号であらわしてください。そうした方が、記号の意味の見通しが良くなるからです。
(2) 高校2年になると、座標点Bの座標値の名前が、名前Bを引き継いだb1などの記号であらわすので、線分OBの長さをbで表します。
三角形の頂点Bに対向する辺OCの長さは、高校1年までとは違って、b以外の記号で(上図ではcと)表します。
【解答】
上図のように、先ず、三角形の辺の直線の方程式を求める。
次に、その方程式のxの係数とyの係数を入れ替えて、一方の係数の正負を逆にすることで、その直線に垂直な直線の方程式を計算する。
その結果、2つの垂線の方程式が、以下のとおりに得られる。
(式1)*b1-(式2)*c1を計算して以下の式を得る。
(注意)D点のx座標が0ということは、AからBCに下ろした垂線にD点が交わることを意味する。すなわち、垂心は3つの直線の交点であることが示されている。
(式3)を式1に代入してy座標を求める。
∴Dの座標は、
上の式の最後の項では、ベクトルAB=ベクトルbとし、ベクトルAC=ベクトルcとした。
上の式の最初の項から、D点の辺BC上の高さは、
である。
リンク:
高校数学の目次
「(佐藤の)数学教科書[三角比・平面図形編]」(東進ブックス)の学習
以下の問14をもう1度解きます。
【問14】△ABCの辺AB,ACをそれぞれ1:2、2:3に内分する点をD,Eとし,BEとCDの交点をFとするとき、
(1)DF:FCを求めよ。
【解答】
メネラウスの定理を証明するための補助線は、他の位置に引いても、
線の長さの比の関係のメネラウスの定理が得られます。
そのため、図形のどこにその補助線を引けば良いか、
もう1つの補助線の位置もおぼえておきましょう。
この問題にメネラウスの定理を適用すべき補助線の位置は、
図に赤線で書きこんだ位置のAGであり、DCに平行な線です。
この位置に補助線を引けばメネラウスの定理が得られますが、
以下では、この補助線を引いたことで分かる線分の長さの比の関係を直接に使って、
(メネラウスの定理を経由せずに)
直接にこの問14を解きます。
線分AGの長さをmとします。
DF=(DB/AB)m=(2/3)m
FC=(EC/AE)m=(3/2)m
DF/FC=((2/3)m)/((3/2)m)
=4/9
∴
DF:FC=4:9
リンク:メネラウスの定理関係
リンク:高校数学の目次
「(佐藤の)数学教科書[三角比・平面図形編]」(東進ブックス)の学習
【問14】△ABCの辺AB,ACをそれぞれ1:2、2:3に内分する点をD,Eとし,BEとCDの交点をFとするとき、
(1)DF:FCを求めよ。
【解答】
メネラウスの定理は、
補助線を良い位置に引けば、線の長さの比の関係のメネラウスの定理が得られる
という定理です。
そのため、図形のどこに補助線を引けば良いか、
図形が回転した位置にあってもわかるようにおぼえておきましょう。
この問題にメネラウスの定理を適用すべき補助線の位置は、
図に赤線で書きこんだ位置のDGであり、BEに平行な線です。
この位置に補助線を引けばメネラウスの定理が得られますが、
以下では、この補助線を引いたことで分かる線分の長さの比の関係を直接に使って、
(メネラウスの定理を経由せずに)
直接にこの問14を解きます。
GE=(DB/AB)・AE=(2/3)AE
DF/FC=GE/EC
=(2/3)AE/EC
=(2/3)・(2/3)
=4/9
∴
DF:FC=4:9
【究極の方法】
上の解き方では、補助線を引いて問題を解きましたが、その補助線を考えるのも面倒くさいと思います。
以下の様に考えると、問題をもっと楽に解けます。
問題の平面図形を3次元空間に配置します。
3次元空間での点の高さを括弧()内に書きます。
上図のように直線BFEの高さを(0)にし、点Aの高さを(6)にします。
3次元空間における直線ADBにおいて、
AD:DB=1:2
の関係があることから、
点Dの高さは(4)になる。
直線AECにおいて、
AE:EC=2:3
の関係があることから、
点Cの高さは(-9)になる。
直線DFCの点間の距離の比については、
点の高さの比を考えると、
DF:FC=4:9
(解答おわり)
リンク:メネラウスの定理関係
リンク:高校数学の目次
【問】上の図形で、点Aから円Oへ引いた2つの接線APとAQが円と接する点PとQを通る直線上の点Bを選ぶ。
(点Aと直線PQとの関係は、以下のように名付けられています。すなわち、点Aが極であり直線PQが極線です。)
そのとき、点Bから円Oへ引いた2つの接線BRとBSが円と接する点RとSを結んだ線分RSの延長線が点Aを通ることを証明せよ。
この問題は難問だと思いますので、以下の解答を見て、証明の仕方を覚えるだけで良いと思います。
円の中心をOとする。
円の中心と各点P,Q,R,Sを結ぶ補助線を引く。
その補助線とその補助線の端と接続する各接線とのなす角度は直角である。
補助線OAを引いて、それと線分PQとの交点をTとする。
線分OAと線分PQは直交する。
補助線OBを引いて、それと線分RSとの交点をUとする。
線分OBと線分RSは直交する。
△OTPと△OPAは、いずれも直角三角形で、2角が等しいから相似である。
そのため、
OT:OP=OP:OA
∴ OT・OA=OP2 (1)
同様にして、△OURと△ORBは相似な直角三角形であるので、
OU・OB=OR2 (2)
円の半径OP=ORである。
この関係を使って、式(1)と式(2)から、以下の関係が得られる。
OT・OA=OU・OB (3)
以下のように、方べきの定理の逆の関係が成り立っている
線分TAの延長線と線分UBの延長線とが点Oで交わり、式(3)の関係があるので、
4点T,A,U,Bは、下図のように、1つの円周上にある。
その新しい円について、
円周角の∠ATB=∠AUB=∠R
∴ UBとUAは直交する。
一方、UBとUSは直交する。
USもUAもUBに直交するので、
USとUAは同一直線上にある。
∴ UAと、点Uを含む線分RSは同一直線上にある。
すなわち、線分RSの延長線が点Aを通る。
(証明終わり)
(この定理の双曲線への応用は、ここをクリックしてジャンプする)。
リンク:
極と極線
ベクトル方程式による極と極線
放物線の極線
放物線の極と極線
複素数平面での円の極と極線
円の性質
方べきの定理の証明
リンク:高校数学の目次
第6講「円の性質」(1)円周角(2/2)
「(佐藤の)数学教科書[三角比・平面図形編]」(東進ブックス)の学習
【定理15】円の弦ABの延長と円周上の点Tにおける接線が点Pで交わるとき、次のことが成り立つ。
PA・PB=PT2
(これを「方べきの定理」と呼ぶ)
【証明】
上図のように書くと、
接弦定理により〇=∠PTA=∠PBT
∠Pは共通だから、
2角相当で、
△PAT∽△PTB
したがって、
PA/PT=PT/PB
すなわち、
PA・PB=PT2
(証明おわり)
《点Pが円内にある場合の方べきの定理》
 リンク:
方べきの定理(の逆)の応用問題1
円の性質
高校数学の目次
リンク:
方べきの定理(の逆)の応用問題1
円の性質
高校数学の目次
以下の問題はやさしいですが、重要な事を伝えているので、大学の図形専門の数学教授が思わず入試問題に出してしまう問題と思います。
【問】上の図形のように円OとO’が点PとQで交差している。上図のように、点Pを通る直線が円O’とAで交わり、円OとはBで交わる。また、点Qを通る直線が円O’とCで交わり、円OとはDで交わる。
このとき、線分ACと線分BDが平行になることを証明せよ。
これに解答するためのヒントの図形を以下に書きます。
リンク:
リンク:高校数学(三角比・図形)一覧
リンク:高校数学の目次
三角形の底辺を垂線で分割した線分の長さの積は垂心の高さに比例する、という垂心の性質があります。
【定理】△ABCの3頂点A,B,Cからそれぞれ直線BC,CA,ABに引いた3本の垂線は1点Hで交わる。
【証明】以下でおぼえやすいと思われる自然な流れの思考パターンでこの定理を証明してみましょう。
上図のように、垂線ADと頂点Bから引いた垂線BEとの交点をHとします。
この図に、同じ角度だとわかる角度と、長さが分かる線の長さをことごとく書き込むと答えが見えてきます。
上図の各線分の長さをa1,a2,h,h1と名づけます。
すると、
三角形BDHと三角形ADCが相似であるので、
h1/a1=a2/h
ゆえに:
交点Hの高さすなわちDHの長さh1=(a2・a1)/h
になります。
この式は、垂線ADと線分BCとの関係だけであらわされています。
同様にして、
頂点Cから線分ABに垂直に引いた垂線と垂線ADとの交点の高さh1’も、
交点の高さh1’=(a2・a1)/h
になります。
そのため、その交点はHと同じ位置になります。
よって、
△ABCの3頂点A,B,Cからそれぞれ直線BC,CA,ABに引いた3本の垂線は1点Hで交わります。
(証明おわり)
リンク:
方べきの定理
三角形の重心
三角形の重心の性質の別解
三角形の外心
三角形の内心
リンク:高校数学(三角形の性質)
リンク:高校数学の目次
【問】三角形の外接円の半径Rを三角形の3辺からもとめる。
この問題は、三角形の外接円の半径が、正弦定理で三角形の1つの角度と関係していることと、
三角形の1つの角度が、余弦定理で三角形の3辺に関係していること
を使えば解けます。
先ず、正弦定理を思い出します。
この正弦定理から、
(1/R)=2sinA/a (1)
が得られます。
次に、三角形の辺の二乗の引き算の公式を変形して余弦定理を導き出して思い出します。
この余弦定理から、
2cosA/a=(b2+c2-a2)/(abc) (2)
が得られます。
sinA2+cosA2=1 (3)
の関係に、この2つの式を代入します。
(1/R)=2sinA/a (1)
2cosA/a=(b2+c2-a2)/(abc) (2)
その代入の準備として、式3を少し変形します。
sinA2+cosA2=1 (3)
((2sinA/a)2+(2cosA/a)2)=(2/a)2 ,
これに、式1と式2を代入します。
(1/R)2+{(b2+c2-a2)/(abc)}2=(2/a)2
この式を(1/R)だけを左辺にした式に変形します。
(1/R)2
=(2/a)2-{(b2+c2-a2)/(abc)}2
《公式P2-Q2=(P-Q)(P+Q)を使う》
={(2/a)-(b2+c2-a2)/(abc)}
{(2/a)+(b2+c2-a2)/(abc)}
={(2bc)-(b2+c2-a2)}
{(2bc)+(b2+c2-a2)}/(abc)2
={(2bc)-b2-c2+a2}
{(2bc)+b2+c2-a2}/(abc)2
={-(b-c)2+a2}{(b+c)2-a2)}/(abc)2
《公式P2-Q2=(P-Q)(P+Q)を使う》
={(-(b-c)+a)((b-c)+a)}
{((b+c)-a)((b+c)+a)}/(abc)2
=(-b+c+a)(b-c+a)
(b+c-a)(b+c+a)/(abc)2
よって、
R2=(abc)2/{(-b+c+a)(b-c+a)(b+c-a)(b+c+a)}
R=(abc)/√{(-b+c+a)(b-c+a)(b+c-a)(b+c+a)}
リンク:
三角形の重心三角形の重心の性質の別解
三角形の外心
三角形の内心
リンク:高校数学(三角形の性質)
リンク:高校数学の目次
(三角形の面積と内接円の半径の関係)
三角形の3つの内角の2等分線は、1点で交わり、その点から3辺までの距離は等しい。
その1点を三角形の内心と呼ぶ。
そして、その内心を中心として3辺に接する円を三角形の内接円とよびます。
【例題】△ABCにおいて、BC=a、CA=b、AB=cとし、内接円の半径をrとするとき、△ABCの面積Sは次の式で表わされることを示せ。
S=r(a+b+c)/2
内接円の中心(内心)をIとすると、
△IBCは、底辺BCに対する高さはrです。
そのため、その面積は a・r/2 です。
同様に、
△ICAも、底辺CAに対する高さはrです。
そのため、その面積は b・r/2 です。
△IABも、底辺ABに対する高さはrです。
そのため、その面積は c・r/2 です。
以上から、△ABCの面積Sは、
S=△IBC+△ICA+△IAB
=r(a+b+c)/2
になります。
(例題おわり)
 三角形のIBCの三角形ABCに対する面積比から、内接円の半径rが上の式のように、三角形の高さhから求められる。
三角形のIBCの三角形ABCに対する面積比から、内接円の半径rが上の式のように、三角形の高さhから求められる。
リンク:
高校数学の目次
「三角錐の重心Oの位置は、その高さの4分の1になります。」
以下に、三角錐の重心の性質の簡単な求め方を示します。
上の図のように、三角錐の重心を3次元座標の原点Oにして考えます。
三角錐ABCDの頂点の座標の平均
(A+B+C+D)/4
が三角錐の重心です。
図のように、A+B+C+D=(0,0,0)となるように座標を定めます。
ここで、三角錐の底面の三角形BCDの重心Gを定めると、
Gの座標は、
G((b+c+d)/3,(e+f+g)/3,(h+k+m)/3)=-A/3
になり、
OGは0Aに平行で長さが3分の1
の関係があることがわかります。
すなわち、AGは重心O点を通ることがわかり、
線分AGが点Oで3:1に分割されることもわかります。
すなわち、
三角錐の重心Oの位置は、その高さの4分の1になる
ことがわかります。
リンク:
高校数学の目次
以下に、三角形の重心の性質の簡単な求め方を示します。
上の図のように、三角形の重心を座標の原点Oにして考えます。
三角形ABCの頂点の座標の平均
(A+B+C)/3
が三角形の重心です。
図のように、A+B+C=(0,0)となるように座標を定めます。
B(b,d)、
C(c,e)、
A(-b-c,-d-e)と座標を定めれば
A+B+C=0になります。
ここで、BCの中点Kを定めると、
Kの座標は、
K((b+c)/2,(d+e)/2)=-A/2
になり、
OKは0Aに平行で長さが2分の1
の関係があることがわかります。
すなわち、AKは重心O点を通ることがわかり、
線分AKが点Oで2:1に分割されることもわかります。
同様な証明のしかたで、三角錐の重心の性質もわかります。
リンク:
高校数学の目次
「(佐藤の)数学教科書[三角比・平面図形編]」(東進ブックス)の学習
三角形の重心の性質の証明は教科書に書いてある通りですが、それを習った上で、
三角形の重心の性質をより速く思いだせるようになるために、
以下の証明方法もおぼえておいてください。
三角形の重心の性質の簡単な証明方法はここをクリック
次に、三角形の重心にかかわる大切な性質を証明する以下の問題を解きます。
【問8】△ABCの重心をOとすると、△OAB、△OBC、△OCAの面積はすべて等しいことを示しなさい。
下の図のように、三角形の各辺の中点と三角形の頂点とを結んだ図を書きます。
重心の性質から、線分OKは線分AKの長さの3分の1ですから、
△OBCの高さは△ABCの高さの3分の1です。
△OBC=△ABC/3
同様に、
△OAB=△ABC/3
△OCA=△ABC/3
そのため、
△OAB、△OBC、△OCAの面積はすべて等しく、△ABC/3になります。
リンク:
高校数学の目次
【問】三角形の3辺の長さがa,b,√(a2+ab+b2)であるとき、最大角の大きさを求めなさい。
【解答開始】
ここで、a,b以外の辺が√(a2+b2)なら角θは90度ですが、その辺がそれより大きいことから、角θは90度以上ということがわかります。
三角形の内角の和は180度ですから、1つの角度が90度より大きければ、それ以外の角度はすべて90度以下です。
そのため、90度より大きい角θがこの三角形の最大角になります。
(余弦定理を思い出す)
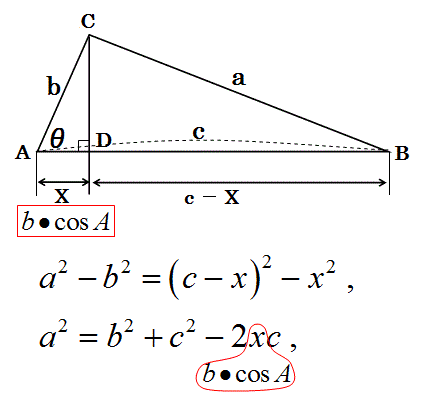 (これが余弦定理)
この余弦定理を使います。
(これが余弦定理)
この余弦定理を使います。
上の図のように辺aと辺bの間の頂点をCとする三角形を書きます。
そして、余弦定理でcos(∠C)=cos(θ)を求めます。
そのcos(θ)の値が-1/2になったので、
角θは120°です。
(解答おわり)
【別解】
三角形の辺の二乗の引き算の公式により:
(解答おわり)
リンク:高校数学の目次
上図のように、AEに平行な補助線QCを引くと
c:b=m:n
となることがわかります。
下図の様に、AEを水平線と考えると、水平線に対してABが成す角とACが成す角が等しい。
リンク:
高校数学の目次
上図のように、ADに平行な補助線PCを引くと
c:b=m:n
となることがわかります。
(つぶれた三角形1)点Aが直線BC上で、辺BC内(点BとCは含まない)にある場合は、つぶれた三角形である。その場合、∠BACは180°になる。その∠BACを2等分する直線ADは辺BCに垂直になる。その場合は、A=Dになる。A=Dの場合は、c=m、b=nになる。しかし、A=Dの場合は、線分ADが1点になってしまうので、線分ADの方向を定める事ができず、∠BACが2等分されているとは言えない。
(つぶれた三角形2)点Aが、直線BC上で、辺BCの外にある場合(点BとCは含まない)は、つぶれた三角形である。その場合は、∠BACは0°になる。その∠BACを二等分する直線ADは直線BCと平行になる。その場合は、Dの辺BC上の位置は定まらない。その場合は、c:b=m:nという関係は無い。
(つぶれた三角形3)点Aが点B又は点Cと一致する場合は、点Aとそれが一致する点を結ぶ線分AB又は線分ACが1点になってしまうので、その線分の方向を定めることができず、∠BACは90°であるとも言えず(∠BAC=0°もあり得る)、∠BACの大きさが定まらない。そのため、∠BACを二等分する直線ADの点Dの辺BC上の位置も定まらない。
そういうわけで、つぶれた三角形の場合には、∠Aを二等分する線分ADに関して、c:b=m:nの関係があるとは言えない。
リンク:
高校数学の目次
【問】次の図において、辺の長さx,yを求めなさい。(3)AD//EF//BC
平行線間の線分の長さの比が同じ。
リンク:高校数学の目次
第4講「図形の計量」(4)球の体積と表面積(その3/3)
「(佐藤の)数学教科書[三角比・平面図形編]」(東進ブックス)の学習
【練習問題23】1辺の長さがaである正四面体について、次の問に答えなさい。
(3)この正四面体に内接する球の半径rを求めなさい。
教科書の解き方が一番良いと思いますが、それとは異なる解き方をしてみます。
正四面体に内接する球の中心は4つの面それぞれから半径rの距離の位置にあります。
それで、Oを頂点として1つの面を底面(面積S)とする三角錐が正四面体の4面の数だけできます。その4つの三角錐の形は合同です。その三角錐の高さはrになります。
そのため、
その三角錐の体積×正四面体の面の数=正四面体の体積(V)になり、
三角錐の体積に関して以下の関係が成り立ちます。
S・r/3=V/4=(S・(正四面体の高さ)/3)/4
この式を変形します。
r=(正四面体の高さ)/4
=((√6)/3)a/4
=((√6)/12)a
(参考)正四面体の重心位置は高さの4分の1
リンク:
高校数学の目次
第4講「図形の計量」(4)球の体積と表面積(その2/3)
「(佐藤の)数学教科書[三角比・平面図形編]」(東進ブックス)の学習
【練習問題23】1辺の長さがaである正四面体について、次の問に答えなさい。
(2)この正四面体に外接する球の半径Rを求めなさい。
図に球の中心Oを書き加えます。
正四面体の重心は、正四面体の高さの4分の1の位置にあります。
正四面体はどの面を底面としても、その高さが同じ図形です。
そのため、正四面体の重心から正四面体の頂点までの長さは、頂点がABCDのどの点であっても同じ長さです。
そのため、重心を中心にする球は正四面体の頂点ABCD全てに接します。
よって、重心を中心とする球は正四面体に外接します。
ゆえに、正四面体に外接する球の半径Rの長さは、正四面体の重心から頂点までの長さであり、
それは、正四面体の高さの3/4です。
そして、正四面体の高さは、(√6/3)aです。
∴R=(3/4)×(√6/3)a
=(√6/4)a
リンク:
高校数学の目次