第６講「円の性質」（２）メネラウスの定理（３／３）
「（佐藤の）数学教科書［三角比・平面図形編］」（東進ブックス）の学習
定理１７ チェバの定理
上の図で
(a1/a2)(b1/b2)(c1/c2)＝１
これがチェバの定理です。
以下、この定理を証明します。
【証明】
上図の赤線のように補助線を引きます。
すると、
△ＲＡＸ∽△ＲＢＹから
u＝(c2/c1)m ・・・（１）
△ＱＡＸ∽△ＱＣＺから
t＝(b1/b2)m ・・・（２）
△ＸＢＹ∽△ＸＺＣから
t＝(a2/a1)u ・・・（３）
式（１）と式（２）からｍを消去する。
(u/t)＝(c2/c1)(b2/b1) ・・・（４）
以下で、式（４）と式（３）からｕ／ｔを消去する。
先ず、式（３）から
(t/u)＝(a2/a1)
これを式（４）に代入する。
(a1/a2)＝(c2/c1)(b2/b1)
∴
(a1/a2)(c1/c2)(b1/b2)＝1
（証明おわり）
チェバの定理の問題点として、以下のあいまいさがあります。以下の図は全てチェバの定理です。これらの場合を全て証明しましたか？
（チェバの定理は、ある使わない点Mと三角形ABCの各々の頂点を結ぶ３本の点線を基準にし、
その各点線まで三角形の所定の辺を延長した図形に対して成り立つ定理です。
３本の点線が三角形の内点Mで束ねられ３辺に交わる場合（内チェバ）と、
３本の点線が三角形の外点Mで束ねられ１辺のみと交わる場合（外チェバ）と
の２種類があります。）
上図の様に、チェバの定理が適用できる図形のパターンは、三角形ABCの辺が延長される辺の数が偶数個あるというパターンがあります。
（一方で、メネラウスの定理が適用できる図形のパターンは、ここをクリックした先にあるように、三角形ABCの辺が延長される辺の数が奇数個あるというパターンがあります。）
【チェバの定理の定義】
高校数学でのチェバの定理の定義があいまいです。定理の定義がはっきりしないので、それは、定理の形を成していません。
そのため、以下でチェバの定理の定義を明確にします。
チェバの定理は：
（１）上の５つの図において、三角形ＡＢＣの各辺毎の３つの直線ＡＢ，ＢＣ，ＣＡと、１つの点M（座標原点）から、各点A,B,Cまで引いた、点線で表した３つの直線（斜交座標軸線）との交点（斜交座標軸点）Ｄ,Ｅ,Ｆを定める。
（２）三角形ＡＢＣの各辺毎の３つの直線上における、交点間の線分の長さの間に、以下の関係がある。
（２ａ）全ての交点を、三角形ＡＢＣの各辺毎の３つの直線同士の交差点である（頂点）Ａ，Ｂ，Ｃと、その（頂点）で無い点の、（斜交座標軸点）Ｄ，Ｅ，Ｆとに分類する。
（２ｂ）そして、全ての交点を、三角形ＡＢＣの各辺毎の３つの直線上をたどる（斜交座標軸線はたどら無い）一筆書きの様な順（線の重なりはOK）で、以下の順に交点を選んで、定理の式を書く。
(頂点)→(斜交座標軸点)→
(頂点)→(斜交座標軸点)→
(頂点)→(斜交座標軸点)→(最初に選んだ頂点)
の順に点を選んで、その定理の式を定義する。
例えば：
(頂点Ａ）→(斜交座標軸点D)→
(頂点Ｂ）→(斜交座標軸点E)→
(頂点Ｃ）→(斜交座標軸点F)→(最初に選んだ頂点Ａ)
の順に選ぶ。
以下の式のように、その選んだ順に点を結んだ線分の間の式を記述し、その式の値を１とする。（ただし、線分の正負の方向性は定めないものとする）
この式がチェバの定理を表す。
（チェバの定理の定義おわり）
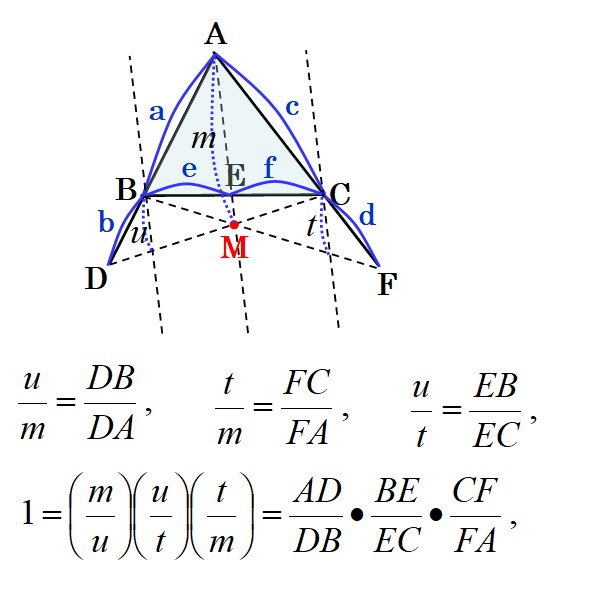
【究極の証明方法】
補助線を引いてチェバの定理を証明するのが面倒くさいので、以下の様に３次元空間を使って証明します。
この平面図形を３次元空間に配置し、
３次元空間での点の高さを括弧（）内に書きます。
上図のように直線ＢＸＱの高さを（０）にし、点Ａの高さを（ｂ２）にし、点Ｃの高さを（－ｂ１）にします。
次に、この図の点Ｐの高さを求めます。
ＡＸ：ＸＰが求められました。
この式を見ると、式にｃ１とｃ２がありません。
図形の左右を入れ替えるとｂとｃが置き換わりますので、
この式をｃであらわすこともできることがわかります。
そのため、同様にして、ＡＸ：ＸＰをｃであらわした式を求めます。
ＡＸ：ＸＰをあわらした以上の２つの式を連立します。
（証明おわり）
《チェバの定理の適用の仕方》
与えられた図形に、チェバの定理の定義に従って、以下の様にチェバの定理を当てはめれば良い。
（１）長さが書き込んである「３つの直線」を求める。
（２）その３つの直線の交差点である３つの（頂点）を求める。
（３）その３つの頂点まで直線で結ぶ原点Ｍを抽出する。その原点Ｍと各頂点を結ぶ直線を斜交座標軸線と認識する。
（４）与えられた図形の点を、３つの直線同士の交差点である（頂点）と、それ以外の、３つの直線と斜交座標軸線との交点（斜交座標軸点）とに分類する。斜交座標軸点が１直線上に並ばないならばチェバの定理が適用できる。もし、斜交座標軸点が一直線上に並ぶ場合は、チェバの定理では無く、メネラウスの定理を適用すべきである。
（５）（頂点）と（斜交座標軸点）を、「３つの直線」上をたどる（斜交座標軸線はたどら無い）一筆書きの様な順（線の重なりはOK）で、以下の順に点を選んで、定理の式を書く。
(頂点)→(斜交座標軸点)→
(頂点)→(斜交座標軸点)→
(頂点)→(斜交座標軸点)→(最初に選んだ頂点)
の順に点を選んで、チェバの定理の式を書く。
（注意）最初に選ぶ点は（斜交座標軸点）では無いことに注意。
リンク：メネラウスの定理等
リンク：高校数学の目次
「（佐藤の）数学教科書［三角比・平面図形編］」（東進ブックス）の学習
定理１７ チェバの定理
(a1/a2)(b1/b2)(c1/c2)＝１
これがチェバの定理です。
以下、この定理を証明します。
【証明】
上図の赤線のように補助線を引きます。
すると、
△ＲＡＸ∽△ＲＢＹから
u＝(c2/c1)m ・・・（１）
△ＱＡＸ∽△ＱＣＺから
t＝(b1/b2)m ・・・（２）
△ＸＢＹ∽△ＸＺＣから
t＝(a2/a1)u ・・・（３）
式（１）と式（２）からｍを消去する。
(u/t)＝(c2/c1)(b2/b1) ・・・（４）
以下で、式（４）と式（３）からｕ／ｔを消去する。
先ず、式（３）から
(t/u)＝(a2/a1)
これを式（４）に代入する。
(a1/a2)＝(c2/c1)(b2/b1)
∴
(a1/a2)(c1/c2)(b1/b2)＝1
（証明おわり）
チェバの定理の問題点として、以下のあいまいさがあります。以下の図は全てチェバの定理です。これらの場合を全て証明しましたか？
（チェバの定理は、ある使わない点Mと三角形ABCの各々の頂点を結ぶ３本の点線を基準にし、
その各点線まで三角形の所定の辺を延長した図形に対して成り立つ定理です。
３本の点線が三角形の内点Mで束ねられ３辺に交わる場合（内チェバ）と、
３本の点線が三角形の外点Mで束ねられ１辺のみと交わる場合（外チェバ）と
の２種類があります。）
上図の様に、チェバの定理が適用できる図形のパターンは、三角形ABCの辺が延長される辺の数が偶数個あるというパターンがあります。
（一方で、メネラウスの定理が適用できる図形のパターンは、ここをクリックした先にあるように、三角形ABCの辺が延長される辺の数が奇数個あるというパターンがあります。）
【チェバの定理の定義】
高校数学でのチェバの定理の定義があいまいです。定理の定義がはっきりしないので、それは、定理の形を成していません。
そのため、以下でチェバの定理の定義を明確にします。
チェバの定理は：
（１）上の５つの図において、三角形ＡＢＣの各辺毎の３つの直線ＡＢ，ＢＣ，ＣＡと、１つの点M（座標原点）から、各点A,B,Cまで引いた、点線で表した３つの直線（斜交座標軸線）との交点（斜交座標軸点）Ｄ,Ｅ,Ｆを定める。
（２）三角形ＡＢＣの各辺毎の３つの直線上における、交点間の線分の長さの間に、以下の関係がある。
（２ａ）全ての交点を、三角形ＡＢＣの各辺毎の３つの直線同士の交差点である（頂点）Ａ，Ｂ，Ｃと、その（頂点）で無い点の、（斜交座標軸点）Ｄ，Ｅ，Ｆとに分類する。
（２ｂ）そして、全ての交点を、三角形ＡＢＣの各辺毎の３つの直線上をたどる（斜交座標軸線はたどら無い）一筆書きの様な順（線の重なりはOK）で、以下の順に交点を選んで、定理の式を書く。
(頂点)→(斜交座標軸点)→
(頂点)→(斜交座標軸点)→
(頂点)→(斜交座標軸点)→(最初に選んだ頂点)
の順に点を選んで、その定理の式を定義する。
例えば：
(頂点Ａ）→(斜交座標軸点D)→
(頂点Ｂ）→(斜交座標軸点E)→
(頂点Ｃ）→(斜交座標軸点F)→(最初に選んだ頂点Ａ)
の順に選ぶ。
以下の式のように、その選んだ順に点を結んだ線分の間の式を記述し、その式の値を１とする。（ただし、線分の正負の方向性は定めないものとする）
この式がチェバの定理を表す。
（チェバの定理の定義おわり）
【究極の証明方法】
補助線を引いてチェバの定理を証明するのが面倒くさいので、以下の様に３次元空間を使って証明します。
３次元空間での点の高さを括弧（）内に書きます。
上図のように直線ＢＸＱの高さを（０）にし、点Ａの高さを（ｂ２）にし、点Ｃの高さを（－ｂ１）にします。
次に、この図の点Ｐの高さを求めます。
この式を見ると、式にｃ１とｃ２がありません。
図形の左右を入れ替えるとｂとｃが置き換わりますので、
この式をｃであらわすこともできることがわかります。
そのため、同様にして、ＡＸ：ＸＰをｃであらわした式を求めます。
ＡＸ：ＸＰをあわらした以上の２つの式を連立します。
《チェバの定理の適用の仕方》
与えられた図形に、チェバの定理の定義に従って、以下の様にチェバの定理を当てはめれば良い。
（１）長さが書き込んである「３つの直線」を求める。
（２）その３つの直線の交差点である３つの（頂点）を求める。
（３）その３つの頂点まで直線で結ぶ原点Ｍを抽出する。その原点Ｍと各頂点を結ぶ直線を斜交座標軸線と認識する。
（４）与えられた図形の点を、３つの直線同士の交差点である（頂点）と、それ以外の、３つの直線と斜交座標軸線との交点（斜交座標軸点）とに分類する。斜交座標軸点が１直線上に並ばないならばチェバの定理が適用できる。もし、斜交座標軸点が一直線上に並ぶ場合は、チェバの定理では無く、メネラウスの定理を適用すべきである。
（５）（頂点）と（斜交座標軸点）を、「３つの直線」上をたどる（斜交座標軸線はたどら無い）一筆書きの様な順（線の重なりはOK）で、以下の順に点を選んで、定理の式を書く。
(頂点)→(斜交座標軸点)→
(頂点)→(斜交座標軸点)→
(頂点)→(斜交座標軸点)→(最初に選んだ頂点)
の順に点を選んで、チェバの定理の式を書く。
（注意）最初に選ぶ点は（斜交座標軸点）では無いことに注意。
リンク：メネラウスの定理等
リンク：高校数学の目次
0 件のコメント:
コメントを投稿