【問】三角形の3辺の長さがa,b,√(a2+ab+b2)であるとき、最大角の大きさを求めなさい。
【解答開始】
ここで、a,b以外の辺が√(a2+b2)なら角θは90度ですが、その辺がそれより大きいことから、角θは90度以上ということがわかります。
三角形の内角の和は180度ですから、1つの角度が90度より大きければ、それ以外の角度はすべて90度以下です。
そのため、90度より大きい角θがこの三角形の最大角になります。
(余弦定理を思い出す)
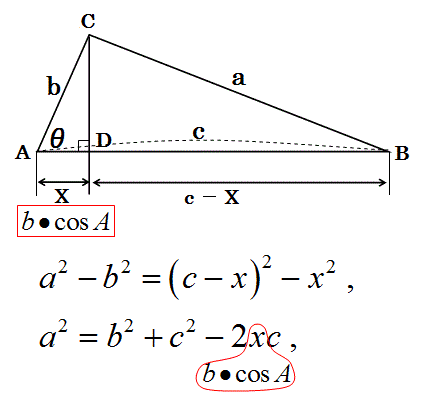
(これが余弦定理)
この余弦定理を使います。
上の図のように辺aと辺bの間の頂点をCとする三角形を書きます。
そして、余弦定理でcos(∠C)=cos(θ)を求めます。
そのcos(θ)の値が-1/2になったので、
角θは120°です。
(解答おわり)
【別解】
三角形の辺の二乗の引き算の公式により:
(解答おわり)
リンク:高校数学の目次
【解答開始】
ここで、a,b以外の辺が√(a2+b2)なら角θは90度ですが、その辺がそれより大きいことから、角θは90度以上ということがわかります。
三角形の内角の和は180度ですから、1つの角度が90度より大きければ、それ以外の角度はすべて90度以下です。
そのため、90度より大きい角θがこの三角形の最大角になります。
(余弦定理を思い出す)
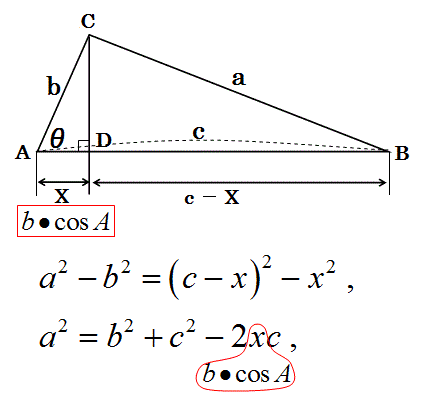
(これが余弦定理)
この余弦定理を使います。
上の図のように辺aと辺bの間の頂点をCとする三角形を書きます。
そして、余弦定理でcos(∠C)=cos(θ)を求めます。
そのcos(θ)の値が-1/2になったので、
角θは120°です。
(解答おわり)
【別解】
三角形の辺の二乗の引き算の公式により:
(解答おわり)
リンク:高校数学の目次



0 件のコメント:
コメントを投稿