円順列とじゅず順列の数を求めます。
問９を少しやさしくした問１０を作りました。
以下でこの問題を解きます。
【問１０】
（１）玉×２個と●２個と○２個を円形に並べる方法（円順列）は何通りあるか。
（２）更に、それらを連結したじゅずを作る方法（じゅず順列）は何通りあるか。
（１）円順列の数は以下の様にして求めます。
玉×と●と○を並べる席が２＋２＋２＝６箇所あります。
６つの席が固定されている場合に、玉×２つと●２つと残りの玉２つを並べる配置の総数は、
６！／（２！×２！×２！）＝６Ｐ４／（２！×２！）
＝６×５×４×３／（２×２）＝９０通り
あります。
（第１のタイプの配置：１／２回転すると元の配置の形に重なる配置）＝周期３の配置パターン
下の２つの円順列の配置では、１／２回転で元の配置の形と同じ形になる。これを第１のタイプの配置とします。
第１のタイプの配置では、１／６回転させる毎に、固定した席に対しては、異なる配置になり、１／２回転するまでに、３つの異なる配置（周期が３）が作られる。
固定席での第１のタイプの配置の数を周期の３で割り算した結果が、第１のタイプの円順列の配置の数です。
第１のタイプの円順列の数は、上図の２組だけです。
これが２組になる計算は、以下の様に計算する。
この、１／２回転すると元の配置の形に重なる配置の玉のパターンは、下図のように、
全部の玉を半分にした、玉×１個と、玉●１個と、玉○１個との３個の玉による、１周期が３である第１の玉の群と、その第１の玉の群を１／２回転した位置の第２の玉の群から成る。
１周期が３であるこの玉の群は、その（固定した３つの席への）玉の配置を上図のようにローテーションさせる毎に、異なる配置になり、席のローテーションにより（固定した３つの席に対して）３つの異なる配置（周期が３）が作られる。
そのため、第１のタイプの（席を固定しないで考える）円順列の数は、以下の計算で求められる。
すなわち、
（固定した席への）配置の数＝３！を、周期の３で割り算した計算：
３！／３＝２
で、第１のタイプの円順列の数を求めることができる。
（第２のタイプの配置：１回転して初めて元の配置の形に重なる配置）＝周期６の配置パターン
玉×と●と○の１つの円順列の配置を１回転すると元の配置の形に重なるが、１／６回転させる毎に、固定した席に対しては、異なる配置になり、１回転するまでに、６つの異なる配置（周期が６）が作られる配置を、第２のタイプの配置とします。
固定席での第２のタイプの配置の数を周期の６で割り算した結果が、第２のタイプの円順列の配置の数です。
第２のタイプの円順列の数は：
（第２のタイプの円順列の数）＝
＝｛固定席での配置の総数－（第１のタイプの円順列の配置の数×３）｝／６
＝｛９０－（２×３）｝／６＝１４
円順列の配置の総数は、この第２のタイプの配置の数に、第１のタイプの円順列の配置の数（２組）を加えた数であり、
１４＋２＝１６
組みです。
《バーンサイドの定理の利用》ここをクリックした先に説明がある。
（バーンサイドの定理の原理）
６つの席に係わる１つの円順列について考える。
（１）回転に対する対称性の無い円順列は、６つの席への６つの角度回転変換（変換数Ｇ＝６）をすることで、（固定席に対して）異なるＧ＝６つの配置パターンに変わる。そのため、
（固定席に対して）全ての異なる配置パターンの数÷Ｇ＝（円順列の数）
という計算で円順列の数を数えることができる。
（２）回転に対してｍ回の対称性があって、６つの角度回転変換（変換数Ｇ＝６）において、（固定席に対する）配置パターンがｍ回繰り返して同じパターンになる円順列は、周期Ｔが、Ｇ／ｍである。その円順列は、（固定席に対して）異なる配置パターンがＧ個は無く、Ｔ＝Ｇ／ｍ個しか無い。
しかし、１回転する間にｍ回同じパターンを繰り返し、周期Ｔ＝Ｇ／ｍまで回転するだけで（１回転しないでも）同じパターンに戻る。そのため周期Ｔ分まで回転する変換においては、その変換によって配置パターンが元の配置パターンに戻る。そのように、その円順列の（固定席への）配置パターンが元のパターンに戻る変換の数は、Ｇ／Ｔ＝ｍ個ある。
そのｍ個の各回転変換では、その変換によって元のパターンに戻る（固定席に対する）配置パターンがＴ個現れる。
その各変換に係わって現れる、（元のパターンに戻る）配置パターンの数Ｔを、それが現れる変換でのＴの数を合計すると、
Ｔ×ｍ＝（Ｇ／ｍ）ｍ＝Ｇ
個になる。そのため、その数をＧで割り算することで、
Ｔ×ｍ／Ｇ＝１
となり、その円順列の数を数えることができる。
（３）結局、
どのような回転変換の対称性のある円順列の数も、
６つの角度回転変換（変換数Ｇ＝６）の１つ毎に、
その変換によって元のパターンに戻る（固定席に対する）配置パターンの数Ｔ個を数え上げて、
Ｇ＝６個の全ての変換毎に現れる元のパターンに戻る配置パターンの数Ｔ個を合計して、
その合計数を、変換の数Ｇで割り算することで円順列の数が求められる。
（４）それゆえ、
全ての円順列の数は、
６つの角度回転変換（変換数Ｇ＝６）の１つ毎に、
その変換によって元のパターンに戻る（固定席に対する）配置パターンの数Ｔ個を数え上げて、
Ｇ＝６個の全ての変換毎のその数Ｔを合計して、
その合計数を、変換の数Ｇで割り算することで全ての円順列の数が求められる。
（これが、バーンサイドの定理の原理である）
以下では、このバーンサイドの定理の原理に従って、全ての円順列の数を数える。
（１）３種類の玉２＋２＋２個の（固定席への）配置のパターンは、
σ0＝０回転、
σ1＝１／６回転、
σ2＝２／６回転、
σ3＝３／６回転、
σ4＝４／６回転、
σ5＝５／６回転、
の変換によって、配置のパターンが変わり得る。
この回転操作の数Ｇ＝６個ある。
（２）このうち、
σ0＝０回転、によってパターンが変わらない配置パターンは、６！／（２！×２！×２！）＝９０個。
σ1＝１／６回転、によってパターンが変わらない配置パターンは、０個。
σ2＝２／６回転、によってパターンが変わらない配置パターンは、０個。
σ3＝３／６回転、によってパターンが変わらない配置パターンは、３！＝６個。
この６個の配置パターンは、以下の、１／２回転で配置が重なる配置パターンである。
（この６個の配置パターンの中に、１／２回転で配置が重なる周期が３の配置の円順列が２つ含まれている）
σ4＝４／６回転、によってパターンが変わらない配置パターンは、０個。
σ5＝５／６回転、によってパターンが変わらない配置パターンは、０個。
（３）バーンサイドの定理によって、
３種類の玉２＋２＋２個の（席を固定しないで考える）円順列の数＝
（９０＋６）／Ｇ＝（９０＋６）／６＝１６個
である。
（解答おわり）
《補足》
このバーンサイド定理で、σ3 に係わる６個の（固定席に対する）配置パターンは、周期が３の２つの円順列に分類できる。
この円順列の数がバーンサイドの定理の式で計算できる理由は、以下のように式が変形できるからです。
（２）じゅず順列の数は以下の様にして求めます。
じゅず順列の場合の数を計算するには、円順列の配置毎に、
円の中心を通る所定の裏返し線でその円順列の配置を裏返す場合に、
裏返した結果が、裏返す前の円順列の配置に重なるかどうかを調べます。
（第３のタイプ：線対称な形の配置）
下図の６個の円順列の配置は、図に書き加えた点線の裏返し線で裏返した結果が裏返す前の元の配置に重なる線対称な形の配置です。
この第３のタイプの円順列の配置の数は６個のみである。その数が、第３のタイプのじゅず順列の配置の数である。
（第４のタイプ：線対称では無い配置）
円順列の配置のうち、第３のタイプの配置以外の配置を第４のタイプの配置とする。
第４のタイプの配置では、円順列では、元の配置と、裏返した後の配置とは異なるので、２倍の数の配置として数えられている。
すなわち、第４のタイプの配置では、円順列の配置の数が、じゅず順列の配置の数の２倍あり、
第４のタイプの配置のじゅず順列の配置の数は、円順列の配置の数を２で割り算した数である。
第４のタイプのじゅず順列の配置の数は：
（（円順列の配置の総数）ー（第３のタイプの円順列の配置の数））／２
＝（１６－６）／２＝５
あります。
一方、第３のタイプの円順列の配置の数＝じゅず順列の配置の数＝６個でした。
全部のじゅず順列の数は、
（じゅず順列の総数）＝
＝（第４のタイプのじゅず順列の配置の数）＋（第３のタイプのじゅず順列の配置の数）
＝５＋６＝１１
《バーンサイドの定理の利用》ここをクリックした先に説明がある。
（１）３種類の玉２＋２＋２個の（固定したじゅずの位置への）配置のパターンに関して、じゅず順列には以下の１２個の変換がある。
σ0＝０回転、
σ1＝１／６回転、
σ2＝２／６回転、
σ3＝３／６回転、
σ4＝４／６回転、
σ5＝５／６回転、
β0＝反転＋０回転、
β1＝反転＋１／６回転、
β2＝反転＋２／６回転、
β3＝反転＋３／６回転、
β4＝反転＋４／６回転、
β5＝反転＋５／６回転、
によって、配置のパターンが変わり得る。
この回転＋反転操作の数Ｇ＝１２個ある。
（２）このうち、
σ0＝０回転、によってパターンが変わらない配置パターンは、６！／（２！×２！×２！）＝９０個。
σ1＝１／６回転、によってパターンが変わらない配置パターンは、０個。
σ2＝２／６回転、によってパターンが変わらない配置パターンは、０個。
σ3＝３／６回転、によってパターンが変わらない配置パターンは、３！＝６個。
σ4＝４／６回転、によってパターンが変わらない配置パターンは、０個。
σ5＝５／６回転、によってパターンが変わらない配置パターンは、０個。
β0＝反転＋０回転、によってパターンが変わらない配置パターンは、３！＝６個。
（反転操作は、図での上下の線（Ｙ軸）を中心にして左右を入れかえる操作と定義する）
β1＝反転＋１／６回転、によってパターンが変わらない配置パターンは、３！＝６個。
β2＝反転＋２／６回転、によってパターンが変わらない配置パターンは、３！＝６個。
β3＝反転＋３／６回転、によってパターンが変わらない配置パターンは、３！＝６個。
β4＝反転＋４／６回転、によってパターンが変わらない配置パターンは、３！＝６個。
β5＝反転＋５／６回転、によってパターンが変わらない配置パターンは、３！＝６個。
ここで、
σ3＝３／６回転、によってパターンが変わらない６個の配置パターンは下図の配置パターンである。
この図で示した６つの配置パターンは、１つの配置パターンを、１／６回転づつ回転させて３個の配置パターンになり、更に、それを反転させて更に３個の配置パターンになり、結局６個の配置パターンになるので、（反転変換と回転変換の周期が６である）１個のじゅず順列の６個の配置パターンである。
この１個のじゅず順列は、反転に対する対称性は無く、
回転に対しては、ｍ＝２回の対称性がある。そして、１２個の反転＋角度回転変換（変換数Ｇ＝１２）において、（固定席に対する）配置パターンが２回繰り返して同じパターンになるじゅず順列である。このじゅず順列の周期Ｔは、Ｇ／ｍ＝１２／２＝６である。そのじゅず順列は、（固定席に対して）異なる配置パターンがＧ＝１２個は無く、Ｔ＝Ｇ／ｍ＝６個しか無い。
しかし、１回転する間にｍ＝２回同じパターンを繰り返し、周期Ｔ＝Ｇ／ｍ＝６回の反転＋回転変換により同じパターンに戻る。そのように、そのじゅず順列の（固定席への）配置パターンが元のパターンに戻る変換の数は、Ｇ／Ｔ＝ｍ＝２個ある。
そのｍ＝２個の各反転＋回転変換毎に、その変換によって元のパターンに戻る（固定席に対する）配置パターンがＴ＝６個現れる。
その各変換に係わって現れる、（元のパターンに戻る）配置パターンの数Ｔ＝６を、それが現れる変換で現れる全てのＴの数を合計すると、
変換σ0＝０回転、では６個。
変換σ3＝３／６回転、では６個。
合計で、
Ｔ×ｍ＝（Ｇ／ｍ）ｍ＝Ｇ＝１２
個になる。
そのため、その数をＧで割り算することで、
Ｔ×ｍ／Ｇ＝１
となり、そのじゅず順列の数を１個と数えることができる。
β0＝反転＋０回転、によってパターンが変わらない（固定席に対する）６個の配置パターンは下図の配置パターンである。
（これは１つのバターンを回転させたパターンではない）
また、左右反転する上下の線（Ｙ軸）と配置のパターンとの位置関係が違うと、
β0＝反転＋０回転、によってパターンが変わらない６個の配置パターンが、以下の６つの配置パターンになる。
反転の定義をしっかりしないといけない問題点がある。
また、このように反転の定義を切り替えて２倍のパターンの１２個の配置パターンを抽出し、その１２個を考察する。この１２個には、反転対称性がある６つのじゅず順列が全て含まれている。しかし、その１２個には、１つのじゅず順列を１／６ずつ回転した全ての配置パターンは網羅されていない。
β1＝反転＋１／６回転、によってパターンが変わらない６個の配置パターン（の１つ）は下図の配置パターンである。
このタイプが（固定席に対しては）６個の配置パターンがある。
この図で示した１個のじゅず順列は、回転に対する対称性は無く、
反転に対しては、ｍ＝２回の反転対称性がある。
そして、１２個の反転＋角度回転変換（変換数Ｇ＝１２）において、（固定席に対する）配置パターンが２回繰り返して同じパターンになるじゅず順列である。このじゅず順列の周期Ｔは、Ｇ／ｍ＝１２／２＝６である。そのじゅず順列は、（固定席に対して）異なる配置パターンがＧ＝１２個は無く、Ｔ＝Ｇ／ｍ＝６個しか無い。
その６個の異なる配置パターンは１／６回転づづの６回の回転による配置パターンの変化である。
しかし、全ての反転＋回転変換において、ｍ＝２回同じパターンを繰り返す。そのように、そのじゅず順列の（固定席への）配置パターンが元のパターンに戻る変換の数は、Ｇ／Ｔ＝ｍ＝２個ある。
しかし、注意すべきことは、このじゅず順列の、（固定席に対して）異なる６個の配置パターンは、１つの反転＋回転変換によって一度に６個が現れたり、１度に２個づつだけ現れる場合もあることである。
各変換に係わって現れる、（元のパターンに戻る）配置パターンの数Ｔ＝６を、それが現れる変換で現れる全てのＴの数を合計すると、
変換σ0＝０回転、では６個。
変換β1＝反転＋１／６回転、では２個。
変換β3＝反転＋３／６回転、では２個。
変換β5＝反転＋５／６回転、では２個。
である。配置パターンの数Ｔ＝６は、変換β1と変換β3と変換β5とに分散して現れて、
その６個の配置パターンと同じ配置パターンが、変換σ0でも現れることで、
合計で、
Ｔ×ｍ＝（Ｇ／ｍ）ｍ＝Ｇ＝１２
個になる。
そのため、その数をＧで割り算することで、
Ｔ×ｍ／Ｇ＝１
となり、そのじゅず順列の数を１個と数えることができる。
β2＝反転＋２／６回転、によってパターンが変わらない６個の配置パターン（の１つ）は下図の配置パターンである。
このタイプが（固定席に対しては）６個の配置パターンがある。
β3＝反転＋３／６回転、によってパターンが変わらない６個の配置パターン（の１つ）は下図の配置パターンである。
このタイプが（固定席に対しては）６個の配置パターンがある。
β4＝反転＋４／６回転、によってパターンが変わらない６個の配置パターン（の１つ）は下図の配置パターンである。
このタイプが（固定席に対しては）６個の配置パターンがある。
β5＝反転＋５／６回転、によってパターンが変わらない６個の配置パターン（の１つ）は下図の配置パターンである。
このタイプが（固定席に対しては）６個の配置パターンがある。
以上の、β0、β1、β2、β3、β4、β5、の変換によってパターンが変わらない配置パターンを抽出することで、反転対称性がある３６個の配置パターンが抽出された。その反転対称性がある３６個の配置パターンを、（回転変換の）周期が６の、６個のじゅず順列のグループに分類できる。
ここで注意すべきことは、反転対称性のある１つのじゅず順列を回転変換した配置パターンが、β0、β1、β2、β3、β4、β5、の変換によってパターンが変わらない配置パターン群の中に分散して存在することである。
例えば、
β2＝反転＋２／６回転、によって変わらないパターンを持つ下図のじゅず順列については：
このじゅず順列を回転した配置パターンは、
β2＝反転＋２／６回転、によって変わらないパターンが２つある。
β4＝反転＋４／６回転、によって変わらないパターンが２つある。
β0＝反転＋０回転、によって変わらないパターンが２つある。
それらの合計６個が同じ１つのじゅず順列をあらわす。
すなわち、１つのじゅず順列を回転変換した６つ配置パターンが、β0、β1、β2、β3、β4、β5、の変換に係わる、各変換によってパターンが変わらない配置パターンのグループの中の、β2のグループとβ4のグループとβ0のグループに分散して存在する。
また、この１つのじゅず順列の（固定席に対する）６つの配置パターンは、変換σ0によってパターンが変わらない配置パターンのグループの中に全部の６個が存在する。
そうして、この１つのじゅず順列を、１２個の全ての反転＋回転変換をすると、変換結果の配置パターンとして、この６個の配置パターンが２回づつ現れる。この１つのじゅず順列の配置の反転対称性ｍが２だから、２回づつ現れるのである。
以上のように、σ0 以外の変換の要素、σ3、β0、β1、β2、β3、β4、β5、の変換によってパターンが変わらない配置パターンを抽出することで、１／２回転対称性のある６個の配置パターン（１個のじゅず順列の配置のバラエティ）と反転対称性がある３６個の配置パターン（６個のじゅず順列の配置のバラエティ）が抽出された。それぞれは、回転変換と反転変換とによって、（固定席に対しては異なる）６個の配置パターンに変わる（変換による配置パターンのバラエティ（周期）が６である）。
それ以外の配置パターンは、回転対称性も反転対称性もない配置パターンである。回転対称性も反転対称性もない配置パターンは、回転変換と反転変換とによって、（固定席に対する）１２個の配置パターンに変わる（周期が１２である）。
（３）バーンサイドの定理によって、
３種類の玉２＋２＋２個の（席を固定しないで考える）配置の基礎パターンの数＝
（９０＋６×７）／Ｇ＝（９０＋４２）／１２＝１１個
である。
【じゅず順列の数の解答（その３）】
円の中心を通る所定の裏返し線で固定席への配置パターンを裏返す（反転変換する）場合に、
反転結果が、反転前の配置に重なるかどうかを調べる。
（第３のタイプのじゅず順列：線対称性を持つ）
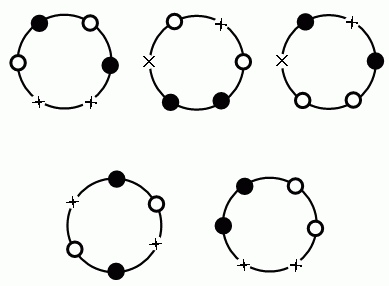
下図の６個のじゅず順列の配置パターン（変換β0、β1、β2、β3、β4、β5 によって配置パターンが変わらないもの）は、図に書き加えた点線の裏返し線で裏返した反転結果が反転前の元の配置に重なる線対称な形の配置である。
この６個の線対象なじゅず順列は、回転変換と反転変換とにより、配置が変えられる配置パターンのバラエティの数が６である。すなわち、１／６回転で６回回転させることで６つの形に変換できる。
（第１のタイプのじゅず順列：１／２回転させると元にもどる回転対称性を持つ）
下の６つの配置パターン（変換σ3 によって配置パターンが変わらないもの）は、１／２回転で元の配置の形と同じ形になる回転対称性がある第１のタイプの配置パターンである。
上図の６つの配置パターンは、反転変換と回転変換によって配置パターンが重なり合う１つのじゅず順列である。
この１つのじゅず順列は、回転変換と反転変換とにより、配置が変えられる配置パターンのバラエティの数（周期）が６である。
以上の７つの、線対象なパターンと、回転対称性があるパターン、とのじゅず順列は、いずれも配置パターンのバラエティ（周期）が６である。
（第５のタイプ：対称性が無い配置）
その７つ以外の、線対象性も無く、回転対称性も無い第５のタイプの配置パターンは、回転変換と反転変換とにより、固定席に対する配置パターンを変えられる配置パターンの数（配置のバラエティの数＝周期）が１２である。
そのため、第５のタイプのじゅず順列の数は、
｛固定席での配置の総数－（第３のタイプのじゅず順列の数＋第１のタイプのじゅず順列の数）×６｝／１２
＝｛９０－（６＋１）×６｝／１２＝４
じゅず順列の配置の総数は、この第５のタイプのじゅず順列の数に、第３のタイプと第１のタイプのじゅず順列の数を加えた数であり、
４＋６＋１＝１１
組みです。
（解答おわり）
このじゅず順列の数がバーンサイドの定理の式で計算できる理由は、以下のように式が変形できるからです。
《補足》
ここで、この問題にバーンサイドの定理の式を使う際に、
（変換β0、β1、β2、β3、β4、β5 によって配置パターンが変わらないもの）
の個数が、それぞれの変換毎に、各々６個あることを調べなければならなかった。その数を調べた上でバーンサイドの定理を使うことができた。
それらの各変換毎に、変換によって配置パターンが変わらない配置の数は、どのようにして調べれば良いのだろうか？
一番良い調べ方は、それらの配置パターンが全て、反転対称性があるじゅず順列であると考えた上で、そのじゅず順列の総数を調べることである。
その目的のために、反転対称性のある（周期が６の）全てのじゅず順列の数（６個）を把握したならば、逆に、
（変換β0、β1、β2、β3、β4、β5 によって配置パターンが変わらないもの）反転対称性のある全てのじゅず順列の（固定席に対する）配置パターンの数が（そのタイプのじゅず順列の数）×（そのタイプのじゅず順列の周期）＝６×６で分かる。それにより、各変換毎に、変換によって変わらない配置パターンの個数を調べる手間が省ける。
よって、この問題をバーンサイドの定理の式を使って解く近道は、先ずは、反転対称性のある（周期が６の）全てのじゅず順列の総数を調べることが近道である。
そして、その目的で、反転対称性のある（周期が６の）全てのじゅず順列の数を調べるのが良い。そして、それば分かれば、
バーンサイドの定理を使わずとも、【じゅず順列の数の解答（その３）】の解き方によって、全てのじゅず順列の数が分かる。その手順で問題を解けば、結局は、問題を解くためにバーンサイドの定理の式を使う必要が無い。
リンク：
バーンサイドの補題を群論の言葉を用いず具体例で説明する＋東大数学・化学の問題をバーンサイドの補題を用いて解く
場合の数と確率
高校数学の目次
問９を少しやさしくした問１０を作りました。
以下でこの問題を解きます。
【問１０】
（１）玉×２個と●２個と○２個を円形に並べる方法（円順列）は何通りあるか。
（２）更に、それらを連結したじゅずを作る方法（じゅず順列）は何通りあるか。
（１）円順列の数は以下の様にして求めます。
玉×と●と○を並べる席が２＋２＋２＝６箇所あります。
６つの席が固定されている場合に、玉×２つと●２つと残りの玉２つを並べる配置の総数は、
６！／（２！×２！×２！）＝６Ｐ４／（２！×２！）
＝６×５×４×３／（２×２）＝９０通り
あります。
（第１のタイプの配置：１／２回転すると元の配置の形に重なる配置）＝周期３の配置パターン
下の２つの円順列の配置では、１／２回転で元の配置の形と同じ形になる。これを第１のタイプの配置とします。
第１のタイプの配置では、１／６回転させる毎に、固定した席に対しては、異なる配置になり、１／２回転するまでに、３つの異なる配置（周期が３）が作られる。
固定席での第１のタイプの配置の数を周期の３で割り算した結果が、第１のタイプの円順列の配置の数です。
第１のタイプの円順列の数は、上図の２組だけです。
これが２組になる計算は、以下の様に計算する。
この、１／２回転すると元の配置の形に重なる配置の玉のパターンは、下図のように、
全部の玉を半分にした、玉×１個と、玉●１個と、玉○１個との３個の玉による、１周期が３である第１の玉の群と、その第１の玉の群を１／２回転した位置の第２の玉の群から成る。
１周期が３であるこの玉の群は、その（固定した３つの席への）玉の配置を上図のようにローテーションさせる毎に、異なる配置になり、席のローテーションにより（固定した３つの席に対して）３つの異なる配置（周期が３）が作られる。
そのため、第１のタイプの（席を固定しないで考える）円順列の数は、以下の計算で求められる。
すなわち、
（固定した席への）配置の数＝３！を、周期の３で割り算した計算：
３！／３＝２
で、第１のタイプの円順列の数を求めることができる。
（第２のタイプの配置：１回転して初めて元の配置の形に重なる配置）＝周期６の配置パターン
玉×と●と○の１つの円順列の配置を１回転すると元の配置の形に重なるが、１／６回転させる毎に、固定した席に対しては、異なる配置になり、１回転するまでに、６つの異なる配置（周期が６）が作られる配置を、第２のタイプの配置とします。
固定席での第２のタイプの配置の数を周期の６で割り算した結果が、第２のタイプの円順列の配置の数です。
第２のタイプの円順列の数は：
（第２のタイプの円順列の数）＝
＝｛固定席での配置の総数－（第１のタイプの円順列の配置の数×３）｝／６
＝｛９０－（２×３）｝／６＝１４
円順列の配置の総数は、この第２のタイプの配置の数に、第１のタイプの円順列の配置の数（２組）を加えた数であり、
１４＋２＝１６
組みです。
《バーンサイドの定理の利用》ここをクリックした先に説明がある。
（バーンサイドの定理の原理）
６つの席に係わる１つの円順列について考える。
（１）回転に対する対称性の無い円順列は、６つの席への６つの角度回転変換（変換数Ｇ＝６）をすることで、（固定席に対して）異なるＧ＝６つの配置パターンに変わる。そのため、
（固定席に対して）全ての異なる配置パターンの数÷Ｇ＝（円順列の数）
という計算で円順列の数を数えることができる。
（２）回転に対してｍ回の対称性があって、６つの角度回転変換（変換数Ｇ＝６）において、（固定席に対する）配置パターンがｍ回繰り返して同じパターンになる円順列は、周期Ｔが、Ｇ／ｍである。その円順列は、（固定席に対して）異なる配置パターンがＧ個は無く、Ｔ＝Ｇ／ｍ個しか無い。
しかし、１回転する間にｍ回同じパターンを繰り返し、周期Ｔ＝Ｇ／ｍまで回転するだけで（１回転しないでも）同じパターンに戻る。そのため周期Ｔ分まで回転する変換においては、その変換によって配置パターンが元の配置パターンに戻る。そのように、その円順列の（固定席への）配置パターンが元のパターンに戻る変換の数は、Ｇ／Ｔ＝ｍ個ある。
そのｍ個の各回転変換では、その変換によって元のパターンに戻る（固定席に対する）配置パターンがＴ個現れる。
その各変換に係わって現れる、（元のパターンに戻る）配置パターンの数Ｔを、それが現れる変換でのＴの数を合計すると、
Ｔ×ｍ＝（Ｇ／ｍ）ｍ＝Ｇ
個になる。そのため、その数をＧで割り算することで、
Ｔ×ｍ／Ｇ＝１
となり、その円順列の数を数えることができる。
（３）結局、
どのような回転変換の対称性のある円順列の数も、
６つの角度回転変換（変換数Ｇ＝６）の１つ毎に、
その変換によって元のパターンに戻る（固定席に対する）配置パターンの数Ｔ個を数え上げて、
Ｇ＝６個の全ての変換毎に現れる元のパターンに戻る配置パターンの数Ｔ個を合計して、
その合計数を、変換の数Ｇで割り算することで円順列の数が求められる。
（４）それゆえ、
全ての円順列の数は、
６つの角度回転変換（変換数Ｇ＝６）の１つ毎に、
その変換によって元のパターンに戻る（固定席に対する）配置パターンの数Ｔ個を数え上げて、
Ｇ＝６個の全ての変換毎のその数Ｔを合計して、
その合計数を、変換の数Ｇで割り算することで全ての円順列の数が求められる。
（これが、バーンサイドの定理の原理である）
以下では、このバーンサイドの定理の原理に従って、全ての円順列の数を数える。
（１）３種類の玉２＋２＋２個の（固定席への）配置のパターンは、
σ0＝０回転、
σ1＝１／６回転、
σ2＝２／６回転、
σ3＝３／６回転、
σ4＝４／６回転、
σ5＝５／６回転、
の変換によって、配置のパターンが変わり得る。
この回転操作の数Ｇ＝６個ある。
（２）このうち、
σ0＝０回転、によってパターンが変わらない配置パターンは、６！／（２！×２！×２！）＝９０個。
σ1＝１／６回転、によってパターンが変わらない配置パターンは、０個。
σ2＝２／６回転、によってパターンが変わらない配置パターンは、０個。
σ3＝３／６回転、によってパターンが変わらない配置パターンは、３！＝６個。
この６個の配置パターンは、以下の、１／２回転で配置が重なる配置パターンである。
（この６個の配置パターンの中に、１／２回転で配置が重なる周期が３の配置の円順列が２つ含まれている）
σ4＝４／６回転、によってパターンが変わらない配置パターンは、０個。
σ5＝５／６回転、によってパターンが変わらない配置パターンは、０個。
（３）バーンサイドの定理によって、
３種類の玉２＋２＋２個の（席を固定しないで考える）円順列の数＝
（９０＋６）／Ｇ＝（９０＋６）／６＝１６個
である。
（解答おわり）
《補足》
このバーンサイド定理で、σ3 に係わる６個の（固定席に対する）配置パターンは、周期が３の２つの円順列に分類できる。
この円順列の数がバーンサイドの定理の式で計算できる理由は、以下のように式が変形できるからです。
（２）じゅず順列の数は以下の様にして求めます。
じゅず順列の場合の数を計算するには、円順列の配置毎に、
円の中心を通る所定の裏返し線でその円順列の配置を裏返す場合に、
裏返した結果が、裏返す前の円順列の配置に重なるかどうかを調べます。
（第３のタイプ：線対称な形の配置）
下図の６個の円順列の配置は、図に書き加えた点線の裏返し線で裏返した結果が裏返す前の元の配置に重なる線対称な形の配置です。
この第３のタイプの円順列の配置の数は６個のみである。その数が、第３のタイプのじゅず順列の配置の数である。
（第４のタイプ：線対称では無い配置）
円順列の配置のうち、第３のタイプの配置以外の配置を第４のタイプの配置とする。
第４のタイプの配置では、円順列では、元の配置と、裏返した後の配置とは異なるので、２倍の数の配置として数えられている。
すなわち、第４のタイプの配置では、円順列の配置の数が、じゅず順列の配置の数の２倍あり、
第４のタイプの配置のじゅず順列の配置の数は、円順列の配置の数を２で割り算した数である。
第４のタイプのじゅず順列の配置の数は：
（（円順列の配置の総数）ー（第３のタイプの円順列の配置の数））／２
＝（１６－６）／２＝５
あります。
一方、第３のタイプの円順列の配置の数＝じゅず順列の配置の数＝６個でした。
全部のじゅず順列の数は、
（じゅず順列の総数）＝
＝（第４のタイプのじゅず順列の配置の数）＋（第３のタイプのじゅず順列の配置の数）
＝５＋６＝１１
《バーンサイドの定理の利用》ここをクリックした先に説明がある。
（１）３種類の玉２＋２＋２個の（固定したじゅずの位置への）配置のパターンに関して、じゅず順列には以下の１２個の変換がある。
σ0＝０回転、
σ1＝１／６回転、
σ2＝２／６回転、
σ3＝３／６回転、
σ4＝４／６回転、
σ5＝５／６回転、
β0＝反転＋０回転、
β1＝反転＋１／６回転、
β2＝反転＋２／６回転、
β3＝反転＋３／６回転、
β4＝反転＋４／６回転、
β5＝反転＋５／６回転、
によって、配置のパターンが変わり得る。
この回転＋反転操作の数Ｇ＝１２個ある。
（２）このうち、
σ0＝０回転、によってパターンが変わらない配置パターンは、６！／（２！×２！×２！）＝９０個。
σ1＝１／６回転、によってパターンが変わらない配置パターンは、０個。
σ2＝２／６回転、によってパターンが変わらない配置パターンは、０個。
σ3＝３／６回転、によってパターンが変わらない配置パターンは、３！＝６個。
σ4＝４／６回転、によってパターンが変わらない配置パターンは、０個。
σ5＝５／６回転、によってパターンが変わらない配置パターンは、０個。
β0＝反転＋０回転、によってパターンが変わらない配置パターンは、３！＝６個。
（反転操作は、図での上下の線（Ｙ軸）を中心にして左右を入れかえる操作と定義する）
β1＝反転＋１／６回転、によってパターンが変わらない配置パターンは、３！＝６個。
β2＝反転＋２／６回転、によってパターンが変わらない配置パターンは、３！＝６個。
β3＝反転＋３／６回転、によってパターンが変わらない配置パターンは、３！＝６個。
β4＝反転＋４／６回転、によってパターンが変わらない配置パターンは、３！＝６個。
β5＝反転＋５／６回転、によってパターンが変わらない配置パターンは、３！＝６個。
ここで、
σ3＝３／６回転、によってパターンが変わらない６個の配置パターンは下図の配置パターンである。
この図で示した６つの配置パターンは、１つの配置パターンを、１／６回転づつ回転させて３個の配置パターンになり、更に、それを反転させて更に３個の配置パターンになり、結局６個の配置パターンになるので、（反転変換と回転変換の周期が６である）１個のじゅず順列の６個の配置パターンである。
この１個のじゅず順列は、反転に対する対称性は無く、
回転に対しては、ｍ＝２回の対称性がある。そして、１２個の反転＋角度回転変換（変換数Ｇ＝１２）において、（固定席に対する）配置パターンが２回繰り返して同じパターンになるじゅず順列である。このじゅず順列の周期Ｔは、Ｇ／ｍ＝１２／２＝６である。そのじゅず順列は、（固定席に対して）異なる配置パターンがＧ＝１２個は無く、Ｔ＝Ｇ／ｍ＝６個しか無い。
しかし、１回転する間にｍ＝２回同じパターンを繰り返し、周期Ｔ＝Ｇ／ｍ＝６回の反転＋回転変換により同じパターンに戻る。そのように、そのじゅず順列の（固定席への）配置パターンが元のパターンに戻る変換の数は、Ｇ／Ｔ＝ｍ＝２個ある。
そのｍ＝２個の各反転＋回転変換毎に、その変換によって元のパターンに戻る（固定席に対する）配置パターンがＴ＝６個現れる。
その各変換に係わって現れる、（元のパターンに戻る）配置パターンの数Ｔ＝６を、それが現れる変換で現れる全てのＴの数を合計すると、
変換σ0＝０回転、では６個。
変換σ3＝３／６回転、では６個。
合計で、
Ｔ×ｍ＝（Ｇ／ｍ）ｍ＝Ｇ＝１２
個になる。
そのため、その数をＧで割り算することで、
Ｔ×ｍ／Ｇ＝１
となり、そのじゅず順列の数を１個と数えることができる。
β0＝反転＋０回転、によってパターンが変わらない（固定席に対する）６個の配置パターンは下図の配置パターンである。
（これは１つのバターンを回転させたパターンではない）
また、左右反転する上下の線（Ｙ軸）と配置のパターンとの位置関係が違うと、
β0＝反転＋０回転、によってパターンが変わらない６個の配置パターンが、以下の６つの配置パターンになる。
反転の定義をしっかりしないといけない問題点がある。
また、このように反転の定義を切り替えて２倍のパターンの１２個の配置パターンを抽出し、その１２個を考察する。この１２個には、反転対称性がある６つのじゅず順列が全て含まれている。しかし、その１２個には、１つのじゅず順列を１／６ずつ回転した全ての配置パターンは網羅されていない。
β1＝反転＋１／６回転、によってパターンが変わらない６個の配置パターン（の１つ）は下図の配置パターンである。
このタイプが（固定席に対しては）６個の配置パターンがある。
この図で示した１個のじゅず順列は、回転に対する対称性は無く、
反転に対しては、ｍ＝２回の反転対称性がある。
そして、１２個の反転＋角度回転変換（変換数Ｇ＝１２）において、（固定席に対する）配置パターンが２回繰り返して同じパターンになるじゅず順列である。このじゅず順列の周期Ｔは、Ｇ／ｍ＝１２／２＝６である。そのじゅず順列は、（固定席に対して）異なる配置パターンがＧ＝１２個は無く、Ｔ＝Ｇ／ｍ＝６個しか無い。
その６個の異なる配置パターンは１／６回転づづの６回の回転による配置パターンの変化である。
しかし、全ての反転＋回転変換において、ｍ＝２回同じパターンを繰り返す。そのように、そのじゅず順列の（固定席への）配置パターンが元のパターンに戻る変換の数は、Ｇ／Ｔ＝ｍ＝２個ある。
しかし、注意すべきことは、このじゅず順列の、（固定席に対して）異なる６個の配置パターンは、１つの反転＋回転変換によって一度に６個が現れたり、１度に２個づつだけ現れる場合もあることである。
各変換に係わって現れる、（元のパターンに戻る）配置パターンの数Ｔ＝６を、それが現れる変換で現れる全てのＴの数を合計すると、
変換σ0＝０回転、では６個。
変換β1＝反転＋１／６回転、では２個。
変換β3＝反転＋３／６回転、では２個。
変換β5＝反転＋５／６回転、では２個。
である。配置パターンの数Ｔ＝６は、変換β1と変換β3と変換β5とに分散して現れて、
その６個の配置パターンと同じ配置パターンが、変換σ0でも現れることで、
合計で、
Ｔ×ｍ＝（Ｇ／ｍ）ｍ＝Ｇ＝１２
個になる。
そのため、その数をＧで割り算することで、
Ｔ×ｍ／Ｇ＝１
となり、そのじゅず順列の数を１個と数えることができる。
β2＝反転＋２／６回転、によってパターンが変わらない６個の配置パターン（の１つ）は下図の配置パターンである。
このタイプが（固定席に対しては）６個の配置パターンがある。
β3＝反転＋３／６回転、によってパターンが変わらない６個の配置パターン（の１つ）は下図の配置パターンである。
このタイプが（固定席に対しては）６個の配置パターンがある。
β4＝反転＋４／６回転、によってパターンが変わらない６個の配置パターン（の１つ）は下図の配置パターンである。
このタイプが（固定席に対しては）６個の配置パターンがある。
β5＝反転＋５／６回転、によってパターンが変わらない６個の配置パターン（の１つ）は下図の配置パターンである。
このタイプが（固定席に対しては）６個の配置パターンがある。
以上の、β0、β1、β2、β3、β4、β5、の変換によってパターンが変わらない配置パターンを抽出することで、反転対称性がある３６個の配置パターンが抽出された。その反転対称性がある３６個の配置パターンを、（回転変換の）周期が６の、６個のじゅず順列のグループに分類できる。
ここで注意すべきことは、反転対称性のある１つのじゅず順列を回転変換した配置パターンが、β0、β1、β2、β3、β4、β5、の変換によってパターンが変わらない配置パターン群の中に分散して存在することである。
例えば、
β2＝反転＋２／６回転、によって変わらないパターンを持つ下図のじゅず順列については：
このじゅず順列を回転した配置パターンは、
β2＝反転＋２／６回転、によって変わらないパターンが２つある。
β4＝反転＋４／６回転、によって変わらないパターンが２つある。
β0＝反転＋０回転、によって変わらないパターンが２つある。
それらの合計６個が同じ１つのじゅず順列をあらわす。
すなわち、１つのじゅず順列を回転変換した６つ配置パターンが、β0、β1、β2、β3、β4、β5、の変換に係わる、各変換によってパターンが変わらない配置パターンのグループの中の、β2のグループとβ4のグループとβ0のグループに分散して存在する。
また、この１つのじゅず順列の（固定席に対する）６つの配置パターンは、変換σ0によってパターンが変わらない配置パターンのグループの中に全部の６個が存在する。
そうして、この１つのじゅず順列を、１２個の全ての反転＋回転変換をすると、変換結果の配置パターンとして、この６個の配置パターンが２回づつ現れる。この１つのじゅず順列の配置の反転対称性ｍが２だから、２回づつ現れるのである。
以上のように、σ0 以外の変換の要素、σ3、β0、β1、β2、β3、β4、β5、の変換によってパターンが変わらない配置パターンを抽出することで、１／２回転対称性のある６個の配置パターン（１個のじゅず順列の配置のバラエティ）と反転対称性がある３６個の配置パターン（６個のじゅず順列の配置のバラエティ）が抽出された。それぞれは、回転変換と反転変換とによって、（固定席に対しては異なる）６個の配置パターンに変わる（変換による配置パターンのバラエティ（周期）が６である）。
それ以外の配置パターンは、回転対称性も反転対称性もない配置パターンである。回転対称性も反転対称性もない配置パターンは、回転変換と反転変換とによって、（固定席に対する）１２個の配置パターンに変わる（周期が１２である）。
（３）バーンサイドの定理によって、
３種類の玉２＋２＋２個の（席を固定しないで考える）配置の基礎パターンの数＝
（９０＋６×７）／Ｇ＝（９０＋４２）／１２＝１１個
である。
【じゅず順列の数の解答（その３）】
円の中心を通る所定の裏返し線で固定席への配置パターンを裏返す（反転変換する）場合に、
反転結果が、反転前の配置に重なるかどうかを調べる。
（第３のタイプのじゅず順列：線対称性を持つ）
下図の６個のじゅず順列の配置パターン（変換β0、β1、β2、β3、β4、β5 によって配置パターンが変わらないもの）は、図に書き加えた点線の裏返し線で裏返した反転結果が反転前の元の配置に重なる線対称な形の配置である。
この６個の線対象なじゅず順列は、回転変換と反転変換とにより、配置が変えられる配置パターンのバラエティの数が６である。すなわち、１／６回転で６回回転させることで６つの形に変換できる。
（第１のタイプのじゅず順列：１／２回転させると元にもどる回転対称性を持つ）
下の６つの配置パターン（変換σ3 によって配置パターンが変わらないもの）は、１／２回転で元の配置の形と同じ形になる回転対称性がある第１のタイプの配置パターンである。
上図の６つの配置パターンは、反転変換と回転変換によって配置パターンが重なり合う１つのじゅず順列である。
この１つのじゅず順列は、回転変換と反転変換とにより、配置が変えられる配置パターンのバラエティの数（周期）が６である。
以上の７つの、線対象なパターンと、回転対称性があるパターン、とのじゅず順列は、いずれも配置パターンのバラエティ（周期）が６である。
（第５のタイプ：対称性が無い配置）
その７つ以外の、線対象性も無く、回転対称性も無い第５のタイプの配置パターンは、回転変換と反転変換とにより、固定席に対する配置パターンを変えられる配置パターンの数（配置のバラエティの数＝周期）が１２である。
そのため、第５のタイプのじゅず順列の数は、
｛固定席での配置の総数－（第３のタイプのじゅず順列の数＋第１のタイプのじゅず順列の数）×６｝／１２
＝｛９０－（６＋１）×６｝／１２＝４
じゅず順列の配置の総数は、この第５のタイプのじゅず順列の数に、第３のタイプと第１のタイプのじゅず順列の数を加えた数であり、
４＋６＋１＝１１
組みです。
（解答おわり）
このじゅず順列の数がバーンサイドの定理の式で計算できる理由は、以下のように式が変形できるからです。
《補足》
ここで、この問題にバーンサイドの定理の式を使う際に、
（変換β0、β1、β2、β3、β4、β5 によって配置パターンが変わらないもの）
の個数が、それぞれの変換毎に、各々６個あることを調べなければならなかった。その数を調べた上でバーンサイドの定理を使うことができた。
それらの各変換毎に、変換によって配置パターンが変わらない配置の数は、どのようにして調べれば良いのだろうか？
一番良い調べ方は、それらの配置パターンが全て、反転対称性があるじゅず順列であると考えた上で、そのじゅず順列の総数を調べることである。
その目的のために、反転対称性のある（周期が６の）全てのじゅず順列の数（６個）を把握したならば、逆に、
（変換β0、β1、β2、β3、β4、β5 によって配置パターンが変わらないもの）反転対称性のある全てのじゅず順列の（固定席に対する）配置パターンの数が（そのタイプのじゅず順列の数）×（そのタイプのじゅず順列の周期）＝６×６で分かる。それにより、各変換毎に、変換によって変わらない配置パターンの個数を調べる手間が省ける。
よって、この問題をバーンサイドの定理の式を使って解く近道は、先ずは、反転対称性のある（周期が６の）全てのじゅず順列の総数を調べることが近道である。
そして、その目的で、反転対称性のある（周期が６の）全てのじゅず順列の数を調べるのが良い。そして、それば分かれば、
バーンサイドの定理を使わずとも、【じゅず順列の数の解答（その３）】の解き方によって、全てのじゅず順列の数が分かる。その手順で問題を解けば、結局は、問題を解くためにバーンサイドの定理の式を使う必要が無い。
リンク：
バーンサイドの補題を群論の言葉を用いず具体例で説明する＋東大数学・化学の問題をバーンサイドの補題を用いて解く
場合の数と確率
高校数学の目次
0 件のコメント:
コメントを投稿