第1講「三角比の考え」(5)サイン,コサインの応用
「佐藤の数学教科書[三角比・平面図形編]」(東進ブックス)の51ページ
三角比をあらわす式:
が得られました。
しかし、この数は二重根号で複雑な形です。
この二重根号の解き方は、通常の検定教科書には記載されていないそうですが、
佐藤の数学教科書の51ページにその解き方が書いてありました。
ここでは、その解き方を、その説明よりも詳しく解説します。
【二重根号の外し方(方法1)】
先ず、
と変形し、その右側の項の形にします。右側の項を、
と仮定した数xとaを求めます。
(以下の計算方針では、√3という数を含んでいない数(x)と(a)を使って表わせる場合の解だけを求める計算をします。
√3を(x)か(a)が含まざるを得なかったら、そこで計算を終わりにする覚悟をして、以下の計算をします)
この式の両辺を二乗します。
と、
がなりたつと考えることができます。
2つ目の式を更に簡単にすると、

1=a2x (2)
になります。
(2)より、
(3)を(1)に代入します。
この式から、
この式4を因数分解して解くと:
(a-1)(a-3)=0
a=1 or 3
a=1の場合を(3)に代入すると、
x=1
よって、
です。
(a=3の場合も:x=1/9になって、それを代入すると同じ答えになります)
そのため、
になりました。
よって、
です。
【二重根号の外し方(方法2)】
二重根号を外すもう1つの方法を説明します。
という形をしている2重根号は、以下の条件が成り立つ場合に外すことができます。
二重根号は外せない場合もありますので、このやり方で外せなかった場合は、それは、二重根号が外せない場合だと思っても良いです。
a=x+y (5)
b=x・y (6)
となるxとyを探します。
そのxとyがあれば、
です。
となるからです。
式5と6の解のx、yを求めるということは、
x2-a・x+b=0 (7)
の解x、yを求めることと同じです。この式7は、式4と同じ式になります。
具体的な今回の以下の問題の場合は、以下のようにして解きます。
の場合は、
と変形します。
この様に、ルートの中の式は、ルートの2倍の項を含む式に変形して、答えを求めます。
を解く場合は、
(x2-4・x+3=0 (式4)を解くのと同じですが)
x+y= a=4=3+1
xy= b=3=3・1
がなりたちますので
x=3
y=1
が見つかりました。
です。
そのため、
です。
リンク:二重根号の外し方の【簡易な計算方法】
リンク:高校数学の目次
「佐藤の数学教科書[三角比・平面図形編]」(東進ブックス)の51ページ
三角比をあらわす式:
が得られました。
しかし、この数は二重根号で複雑な形です。
この二重根号の解き方は、通常の検定教科書には記載されていないそうですが、
佐藤の数学教科書の51ページにその解き方が書いてありました。
ここでは、その解き方を、その説明よりも詳しく解説します。
【二重根号の外し方(方法1)】
先ず、
と変形し、その右側の項の形にします。右側の項を、
と仮定した数xとaを求めます。
(以下の計算方針では、√3という数を含んでいない数(x)と(a)を使って表わせる場合の解だけを求める計算をします。
√3を(x)か(a)が含まざるを得なかったら、そこで計算を終わりにする覚悟をして、以下の計算をします)
この式の両辺を二乗します。
(x)と(a)とが√3を含んでいない数であらわされるならば、
4=a・(1+3x) (1)と、
がなりたつと考えることができます。
2つ目の式を更に簡単にすると、

1=a2x (2)
になります。
(2)より、
(3)を(1)に代入します。
この式から、
この式4を因数分解して解くと:
(a-1)(a-3)=0
a=1 or 3
a=1の場合を(3)に代入すると、
x=1
よって、
です。
(a=3の場合も:x=1/9になって、それを代入すると同じ答えになります)
そのため、
になりました。
よって、
です。
【二重根号の外し方(方法2)】
二重根号を外すもう1つの方法を説明します。
という形をしている2重根号は、以下の条件が成り立つ場合に外すことができます。
二重根号は外せない場合もありますので、このやり方で外せなかった場合は、それは、二重根号が外せない場合だと思っても良いです。
a=x+y (5)
b=x・y (6)
となるxとyを探します。
そのxとyがあれば、
です。
となるからです。
式5と6の解のx、yを求めるということは、
x2-a・x+b=0 (7)
の解x、yを求めることと同じです。この式7は、式4と同じ式になります。
具体的な今回の以下の問題の場合は、以下のようにして解きます。
の場合は、
と変形します。
この様に、ルートの中の式は、ルートの2倍の項を含む式に変形して、答えを求めます。
を解く場合は、
(x2-4・x+3=0 (式4)を解くのと同じですが)
x+y= a=4=3+1
xy= b=3=3・1
がなりたちますので
x=3
y=1
が見つかりました。
です。
そのため、
です。
リンク:二重根号の外し方の【簡易な計算方法】
リンク:高校数学の目次

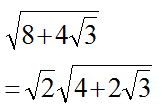



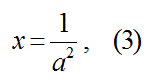

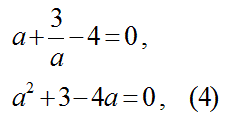










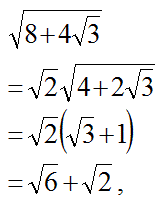
0 件のコメント:
コメントを投稿