中学生の時は数学ができたのに、高校生になって、正弦定理や余弦定理が覚えられない(時が経つと忘れてしまう)ので数学の勉強で挫折する学生が多いらしい。
「覚えられない(忘れてしまう)」で挫折するのは、数学を、公式を覚える学問だと認識していたから、急に数学が出来なくなったものと誤解するからだと思います。しかし、それは間違った認識だと思います。数学は公式を覚える学問では無く、公式を導き出す学問だと思います。
中学生のときから、数学の公式は覚えられない(時が経つと忘れる)ものだと知っていた学生は、公式が覚えられない(忘れる)のは当たり前の事だと認識しています。そして、公式を覚えるというより、公式を導き出して使う練習をして来ていたと思います。
そのため、高校生になって初めて「公式が覚えられない」という真実に気付いた学生は、挫折するのでは無く、公式を導き出すことを覚えて欲しいと思います。
下図のように三角形の周りに、その外接円とその円の中心(外心)とを描きます。
上の図で、三角形の頂点の角度∠A=θが外接円の円周角であり、それは中心角∠BOCの2分の1であることに注目すると、
三角形の外接円の半径Rと、三角形の頂点の角度∠A=θとその頂点Aへの対辺の長さaとの間に、以下の関係式が成り立つことがわかります。
すなわち、∠A=θの対辺の長さをaとすると、
この式を変形すると、
です。
「覚えられない(忘れてしまう)」で挫折するのは、数学を、公式を覚える学問だと認識していたから、急に数学が出来なくなったものと誤解するからだと思います。しかし、それは間違った認識だと思います。数学は公式を覚える学問では無く、公式を導き出す学問だと思います。
中学生のときから、数学の公式は覚えられない(時が経つと忘れる)ものだと知っていた学生は、公式が覚えられない(忘れる)のは当たり前の事だと認識しています。そして、公式を覚えるというより、公式を導き出して使う練習をして来ていたと思います。
そのため、高校生になって初めて「公式が覚えられない」という真実に気付いた学生は、挫折するのでは無く、公式を導き出すことを覚えて欲しいと思います。
下図のように三角形の周りに、その外接円とその円の中心(外心)とを描きます。
上の図で、三角形の頂点の角度∠A=θが外接円の円周角であり、それは中心角∠BOCの2分の1であることに注目すると、
三角形の外接円の半径Rと、三角形の頂点の角度∠A=θとその頂点Aへの対辺の長さaとの間に、以下の関係式が成り立つことがわかります。
すなわち、∠A=θの対辺の長さをaとすると、
この式を変形すると、
同様に、
∠Bの対辺の長さをbとし、
∠Cの対辺の長さをcとすると、
が成り立ちます。
これらをまとめて正弦定理と呼びます。
正弦定理は、上の図の様に、円周角の定理と密接に結びついた定理です。
円周角に関係が深い問題は正弦定理を使って解きましょう。
(後に学ぶ余弦定理は円周角に関する問題を解くのが苦手で、高校2年で学ぶベクトル方程式も円周角に関する問題を解くのが苦手です。それらの問題に正弦定理を使って解いてください。)
以下の図を書けば、正弦定理を確実に思い出すことができると思います。
上図の円と直角二等辺三角形を思い浮かべ、上の正弦定理の式を連想して思い出すようにしましょう。
以下のシンボルマークを計算用紙の片隅に書いて、連想して正弦定理を思い出しましょう。
正弦定理は、三角形の辺と角度の間の以下の関係式も正弦定理です。
【正弦定理のやさしい覚え方】
上の図で、a・sin(B)も、b・sin(A)も、ともに、
頂点Cから辺cに垂直に下ろした線の長さをあらわしますので、両者は等しいです。
a・sin(B)=b・sin(A) (正弦定理)
この式のように、外接円の半径を省いた形の正弦定理でも、十分に応用できます。
また、正弦定理とその他の定理を合わせると、ここをクリックした先のページの様に、三角形の垂心の図の全ての線分を三角関数の積で表すことができます。
リンク:
裏正弦定理
余弦定理の1番やさしい覚え方
余弦定理の2番目にやさしい覚え方
余弦定理の確実な思い出し方
sinθとcosθの連立方程式で式からθを除去する方法
三角形の重心
三角形の垂心
三角形の内心
高校数学(三角比・図形)一覧
高校数学の目次
∠Bの対辺の長さをbとし、
∠Cの対辺の長さをcとすると、
が成り立ちます。
これらをまとめて正弦定理と呼びます。
正弦定理は、上の図の様に、円周角の定理と密接に結びついた定理です。
円周角に関係が深い問題は正弦定理を使って解きましょう。
(後に学ぶ余弦定理は円周角に関する問題を解くのが苦手で、高校2年で学ぶベクトル方程式も円周角に関する問題を解くのが苦手です。それらの問題に正弦定理を使って解いてください。)
以下の図を書けば、正弦定理を確実に思い出すことができると思います。
上図の円と直角二等辺三角形を思い浮かべ、上の正弦定理の式を連想して思い出すようにしましょう。
以下のシンボルマークを計算用紙の片隅に書いて、連想して正弦定理を思い出しましょう。
正弦定理は、三角形の辺と角度の間の以下の関係式も正弦定理です。
【正弦定理のやさしい覚え方】
上の図で、a・sin(B)も、b・sin(A)も、ともに、
頂点Cから辺cに垂直に下ろした線の長さをあらわしますので、両者は等しいです。
a・sin(B)=b・sin(A) (正弦定理)
この式のように、外接円の半径を省いた形の正弦定理でも、十分に応用できます。
また、正弦定理とその他の定理を合わせると、ここをクリックした先のページの様に、三角形の垂心の図の全ての線分を三角関数の積で表すことができます。
リンク:
裏正弦定理
余弦定理の1番やさしい覚え方
余弦定理の2番目にやさしい覚え方
余弦定理の確実な思い出し方
sinθとcosθの連立方程式で式からθを除去する方法
三角形の重心
三角形の垂心
三角形の内心
高校数学(三角比・図形)一覧
高校数学の目次








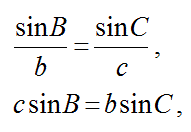

0 件のコメント:
コメントを投稿